ベクトルを超基本から説明します。
目次
有向線分とベクトルの違い
数値だけ示したい
長さや質量は、単位さえ決めておけば、その大きさは、数値で表すことができます。
たとえば、長さを表す場合、1メートルの単位を決めておけば、その2倍が「2メートル」、3倍が「3メートル」という具合です。
さて、この大きさを視覚的に表すには、長さが限られている「線分」を使うのが適当です。
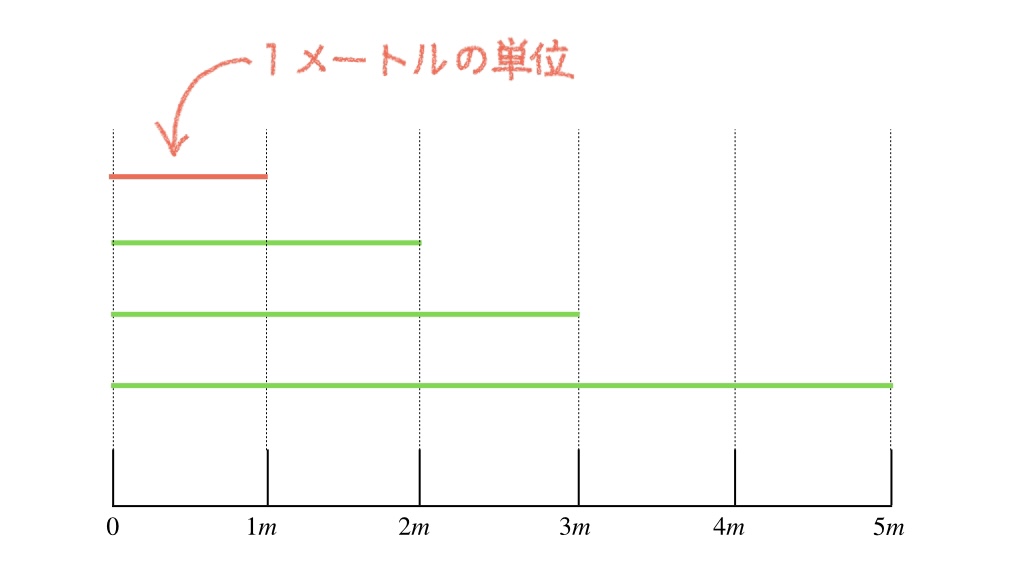
単位の長さの線分を決めておけば、その何倍なのかは線分の長さを比べれば見当がつきます。
しかし、日常生活では「リボンを2メートル買ってきて」のように、その数値さえ示せばいい場合もありますが、それでは困るときもあります。
数値だけでなく方向も示したい
たとえば「駅から2キロメートル歩く」という場合、同じ2キロメートルでも「駅から東に2キロメートル」と「駅から西に2キロメートル」では、到着地点が全く異なってしまいます。
この西や東などの向きの違いを示すには矢印が有効です。そして、距離などの数値を矢印の長さで表すことにすれば、向きと数値の両方を表せるので一石二鳥です。
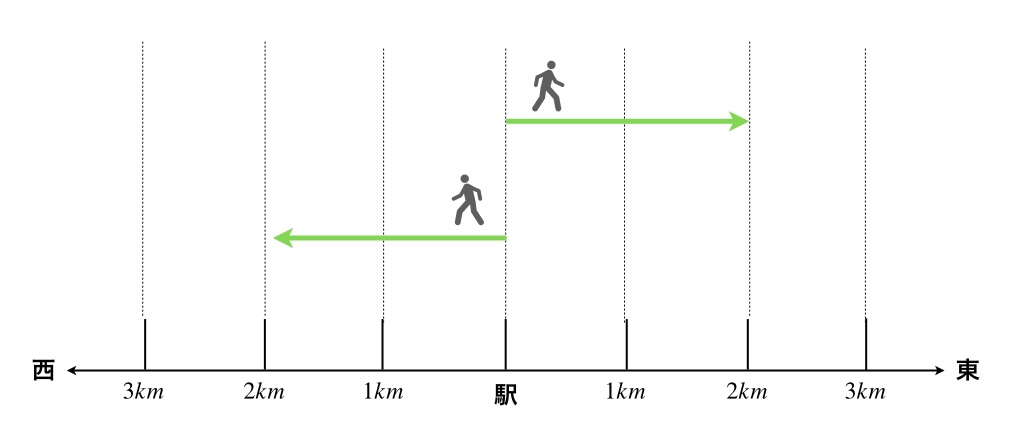
矢印の始点を駅、つまり出発点におけば、矢印の終点が目的地になります。
このように「位置」と「向き」と「大きさ」を表すには「有向線分」を使います。有向線分は、その名の通り「向き」がある「線分」のことです。
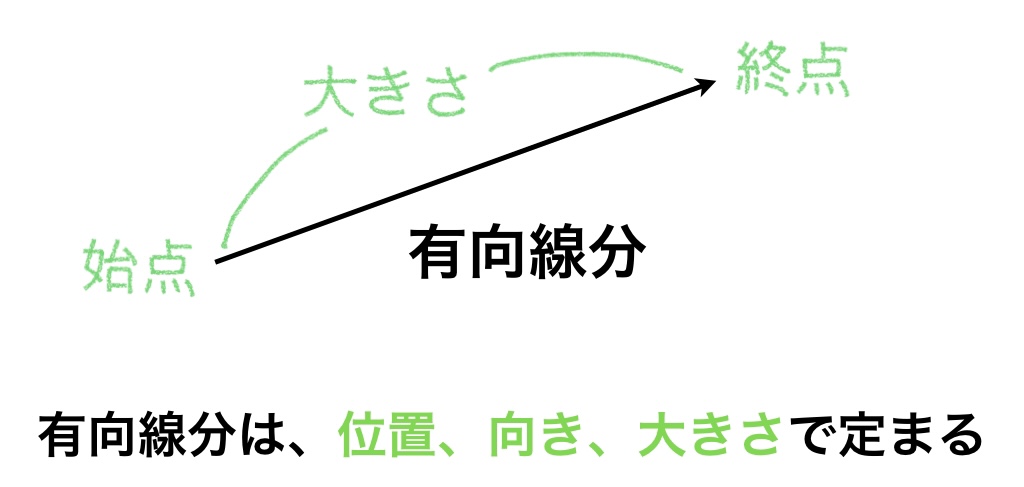
この有向線分の位置を決めずに「向き」と「大きさ」だけで定めるものをベクトルと呼びます。つまり始点と終点の位置を定めません。
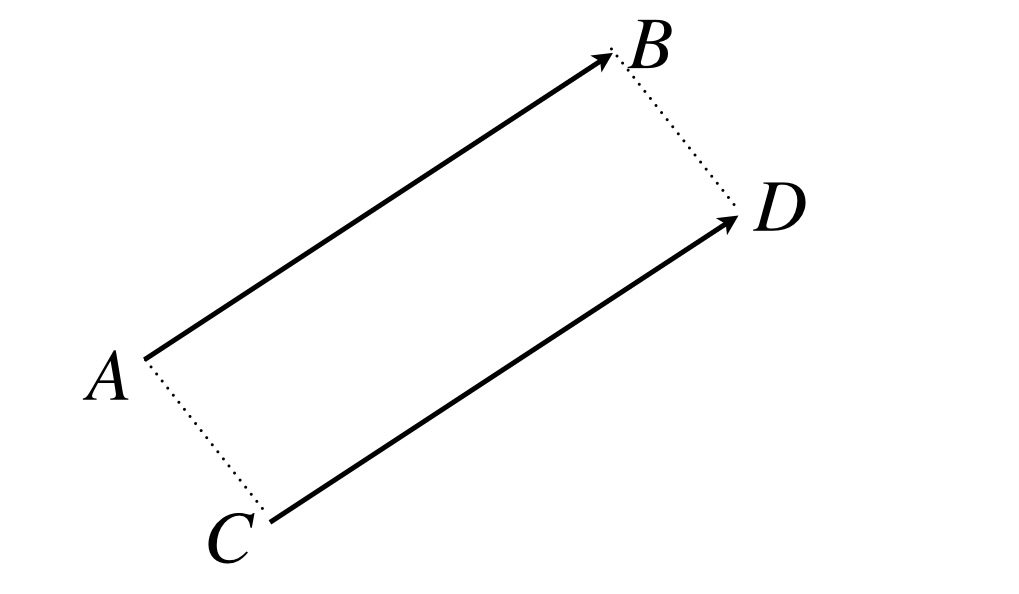
有効線分は、始点と終点が決まれば、たったひとつに決まるので身動きができませんが、ベクトルは、「方向」と「大きさ」しか定めないので、このふたつを保ったままなら自由に動き回れます。ですから、次の図のように、平行移動してピッタリと重なるなら、有効線分としては違っていても、ベクトルとしては同じになります。
では、なぜ出発点を除いて動けるようにするのかというと、このことによってベクトルの計算が可能になるからです。
ベクトルの計算ができることによって、図形問題が計算で解けるようになります。これがベクトルのスゴい点です。
ベクトルの計算ができるようにするためには、計算式を作るためのベクトルの表記方法を決めておかなければなりません。
では、どのようにベクトルを表記するのか見ていきましょう。
ベクトルの表し方
ベクトルを意味する文字
ベクトルは文字と矢印で表します。ふつう文字の上に矢印を書きます。
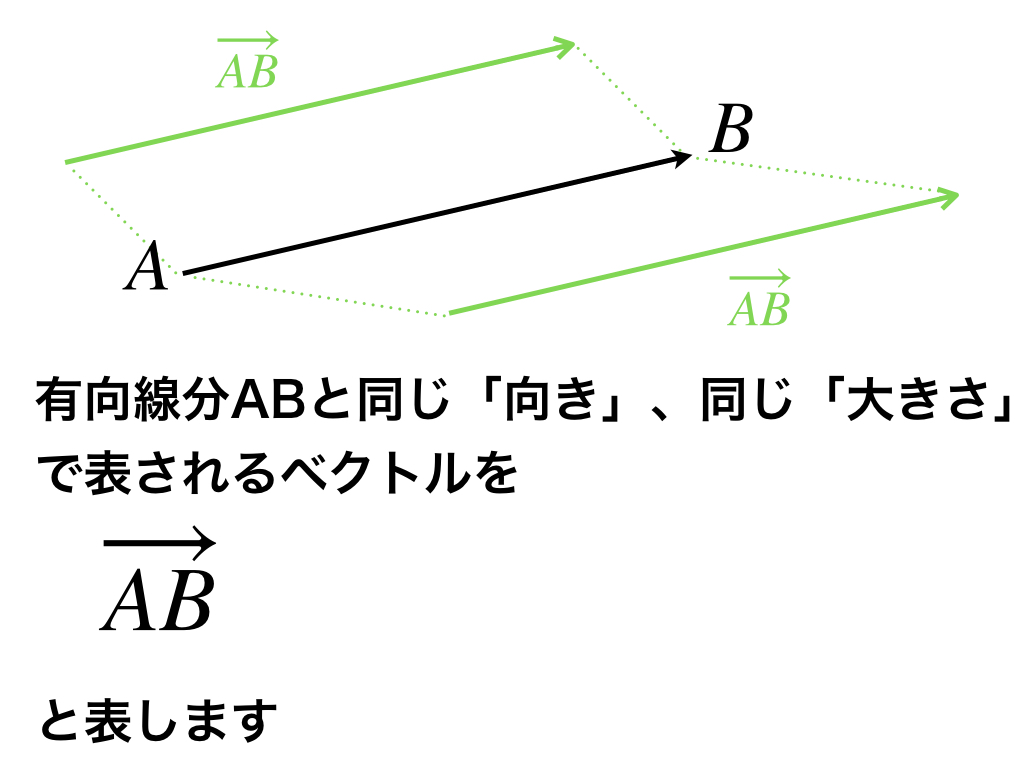
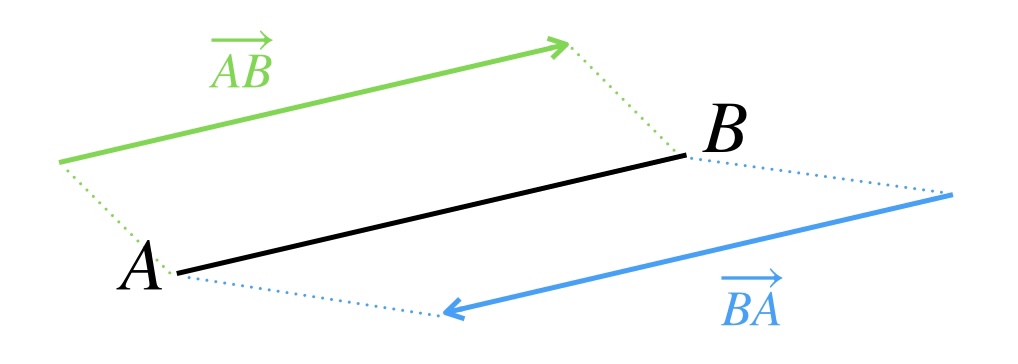
ところで、ベクトルABとベクトルBAは違う点に注意しましょう。ベクトルの向きが反対です。
また、ベクトルは、ひとつの文字と矢印を用いて次のように表すこともできます。
ベクトルの大きさ
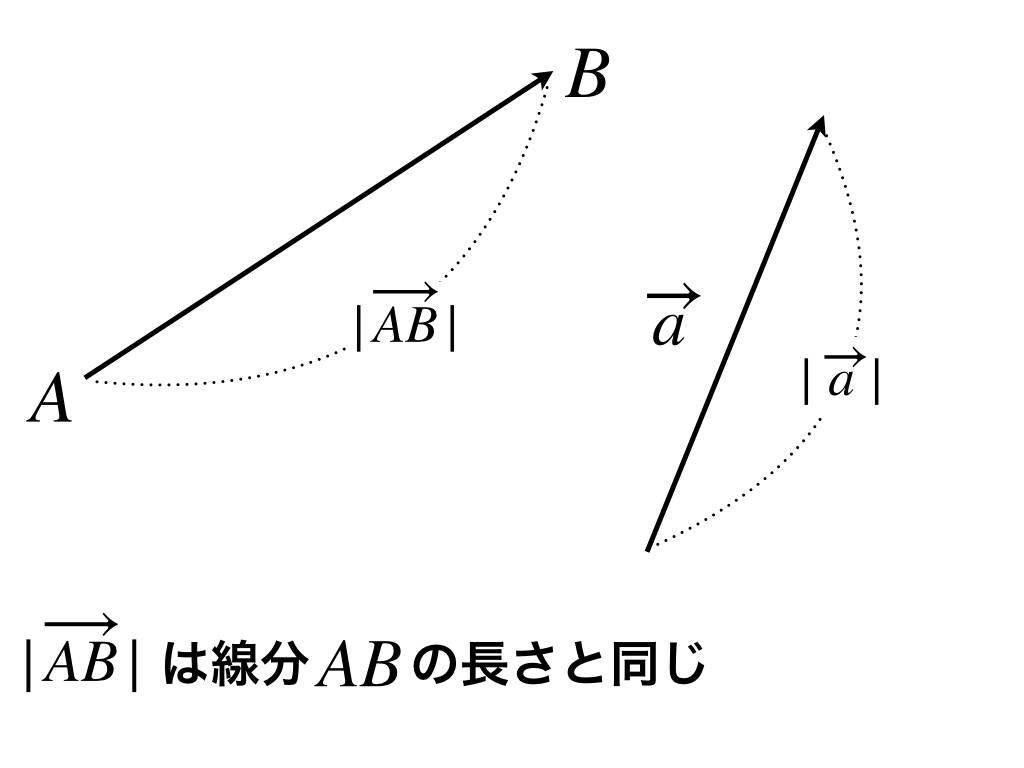
ベクトルの「向き」を無効にして、「大きさ」だけを表したい場合は、絶対値記号を使って、次のように書きます。
ベクトルの相当
ふたつのベクトルの「向き」と「大きさ」が同じならば、そのふたつのベクトルは「等しい」ことになります。その場合、次のように書きます。
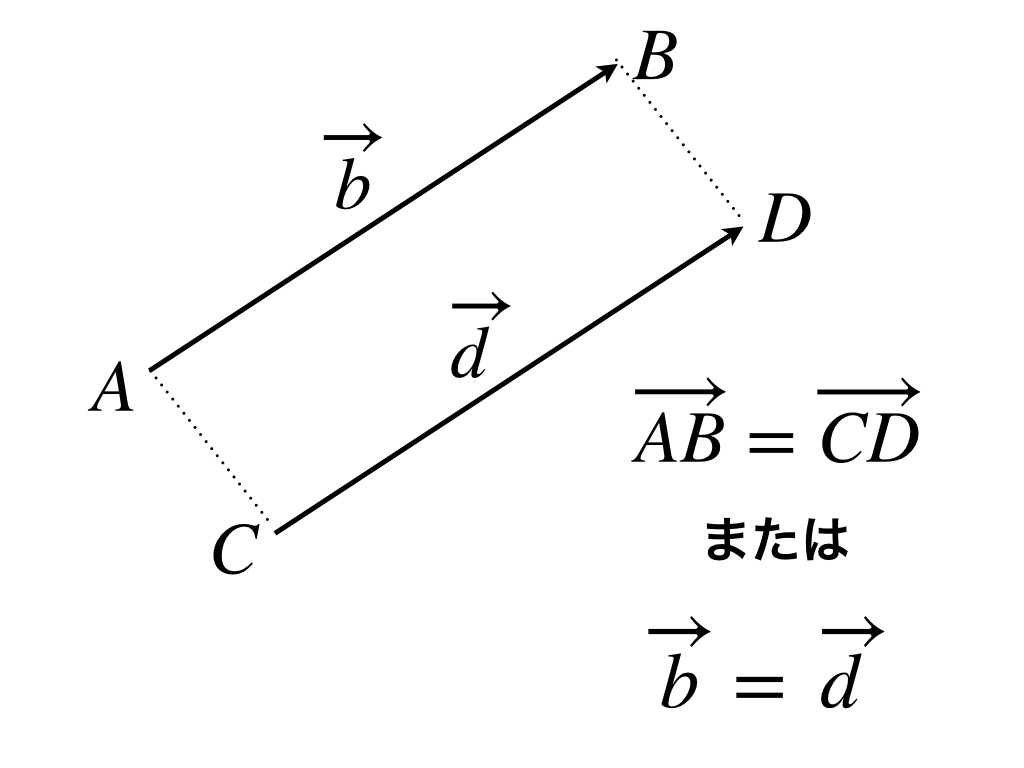
ベクトルが等しければ、ふたつのベクトルをイコールで結べばいいのですね。
ベクトルの演算
では、ベクトルの計算を考えていきましょう。最初は加法(たし算)からです。
ベクトルの加法
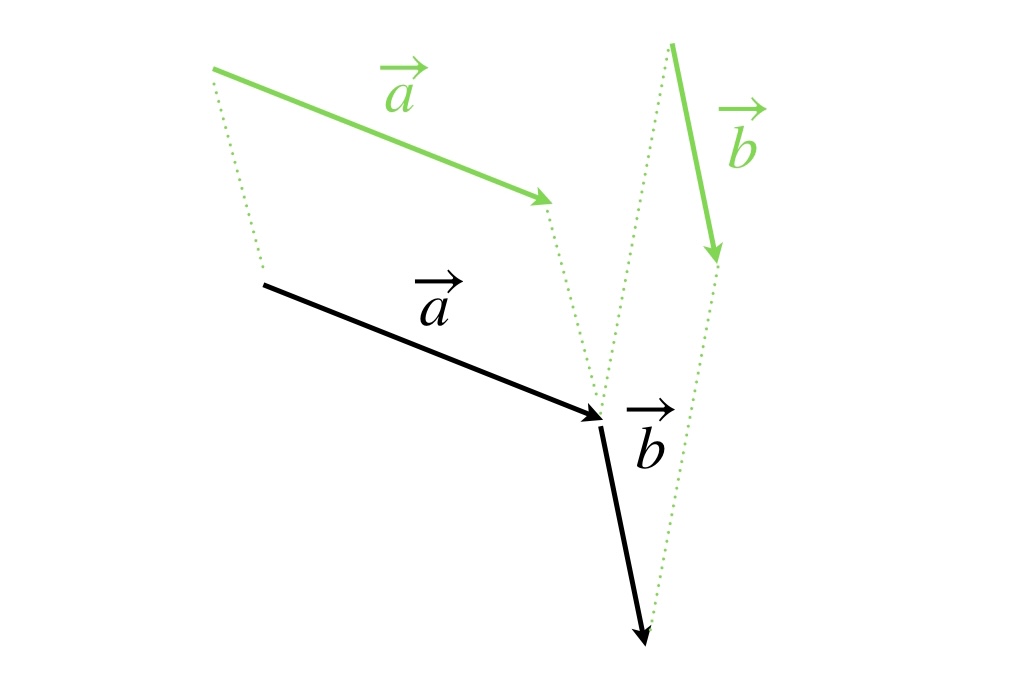
次のふたつのベクトルの和を考えましょう。

ベクトルは「大きさ」と「向き」を変えなければ移動してもいいので、下の図のようにそれぞれのベクトルを平行移動させて連結します。
このとき、ベクトルの連結の仕方に注意して下さい。必ずベクトルの矢印の先端が次のベクトルの矢印の後端につながるようにします。
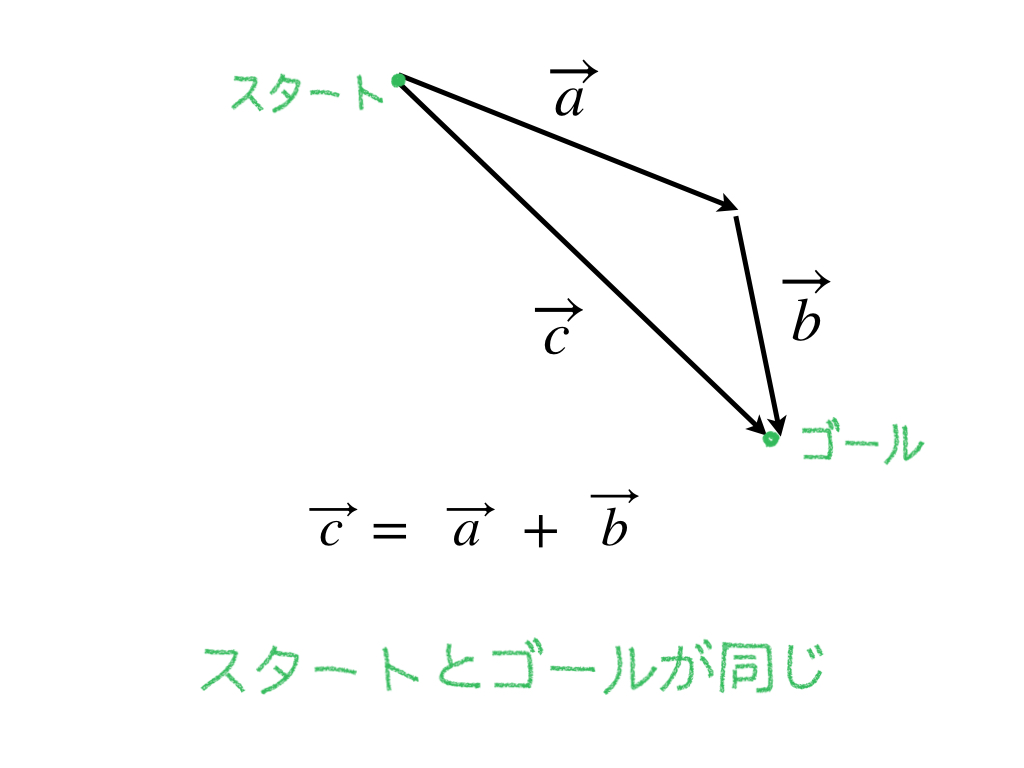
そして図のようにスタートとゴールが同じベクトルをもうひとつ考えます。このベクトルが、最初にあったふたつのベクトルの和と同じベクトルになります。
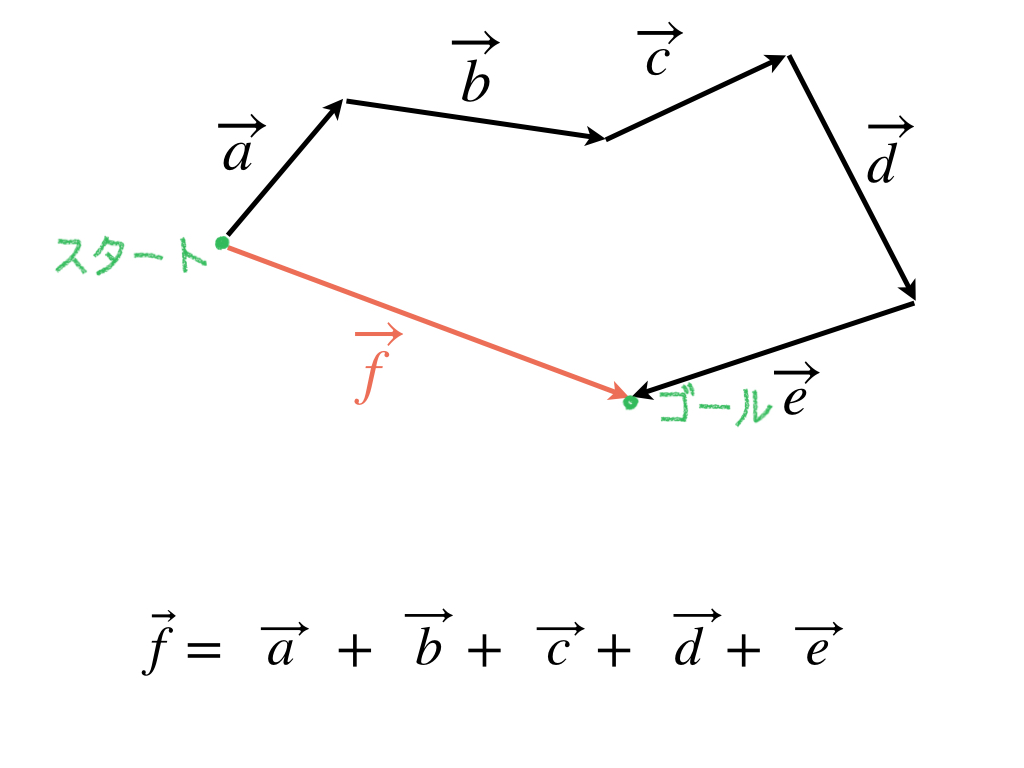
3つ以上のベクトルの和も、スタートとゴールが同じベクトルを考えればよいのです。
ベクトルの加法には、交換法則と結合法則が成り立ちます。
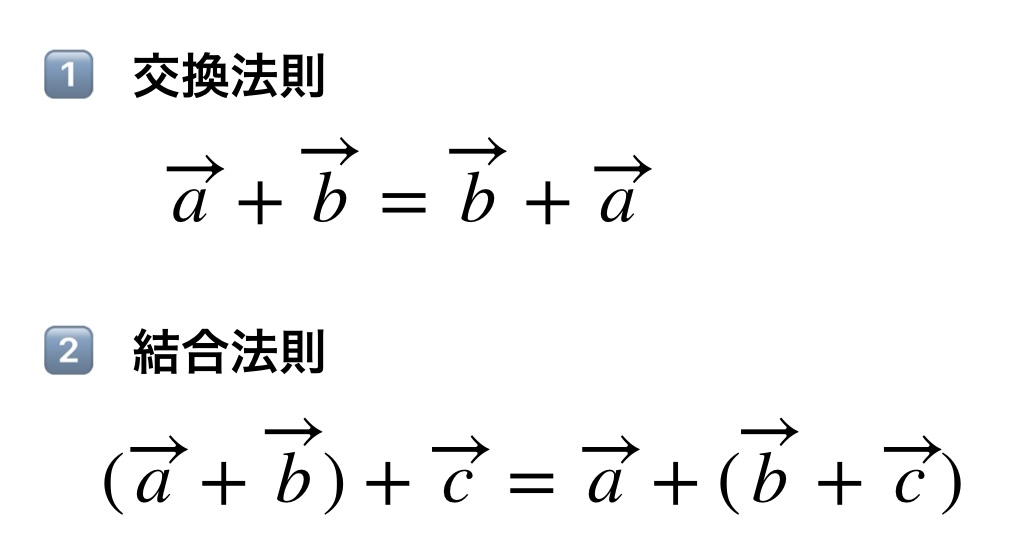
逆ベクトルと零ベクトル(ゼロベクトル)
逆ベクトル
あるベクトルに対して、大きさが等しく、向きが反対であるベクトルを、もとのベクトルの逆ベクトルと言います。

つまりマイナスの記号は元のベクトルの反対向きを意味します。
零ベクトル (ゼロベクトル)
有向線分で、始点と終点が一致してしまうと、大きさが0(ゼロ)になってしまいます。

矢印が描けなくなってしまいましたね。このように大きさが0(ゼロ)のベクトルを零ベクトル、またはゼロベクトルと呼びます。零ベクトルは、次のように0(ゼロ)の上に矢印を書いて表します。

零ベクトルの向きは考えません。
この「考えない」とは「向きがない」とは違います。向きがなかったらベクトルでは無くなってしまうからです。
零ベクトル (ゼロベクトル) の場合「向き」という項目はあるけれども、その具体的方向は考えても意味がないので「考えない」のです。
ですから矢印がない、ただの0(ゼロ)、すなわちスカラー量の0(ゼロ)とは明確に区別しなければなりません。零ベクトル(ゼロベクトル) は、あくまでもベクトルの世界での0(ゼロ)なのです。
零ベクトル(ゼロベクトル)の大きさは0(ゼロ)です。
逆ベクトルと零ベクトル(ゼロベクトル)には、次のような性質があります。

ベクトルの減法
次はベクトルの減法(引き算)です。
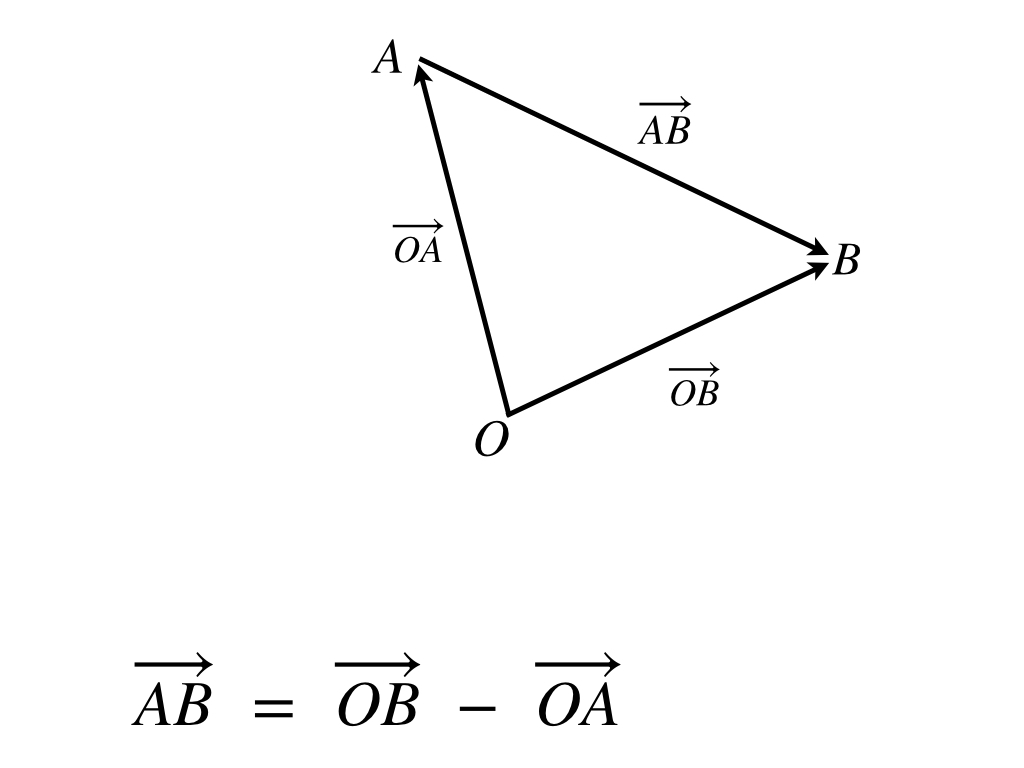
これは次のように考えて下さい。任意の点Oを用意して、その点からベクトルのスタートとゴールを指し示すベクトルを考えます(これを位置ベクトルと言います)。
ゴールを示す位置ベクトルからスタートを示す位置ベクトルを引けば、それが元のベクトルと同じになります。
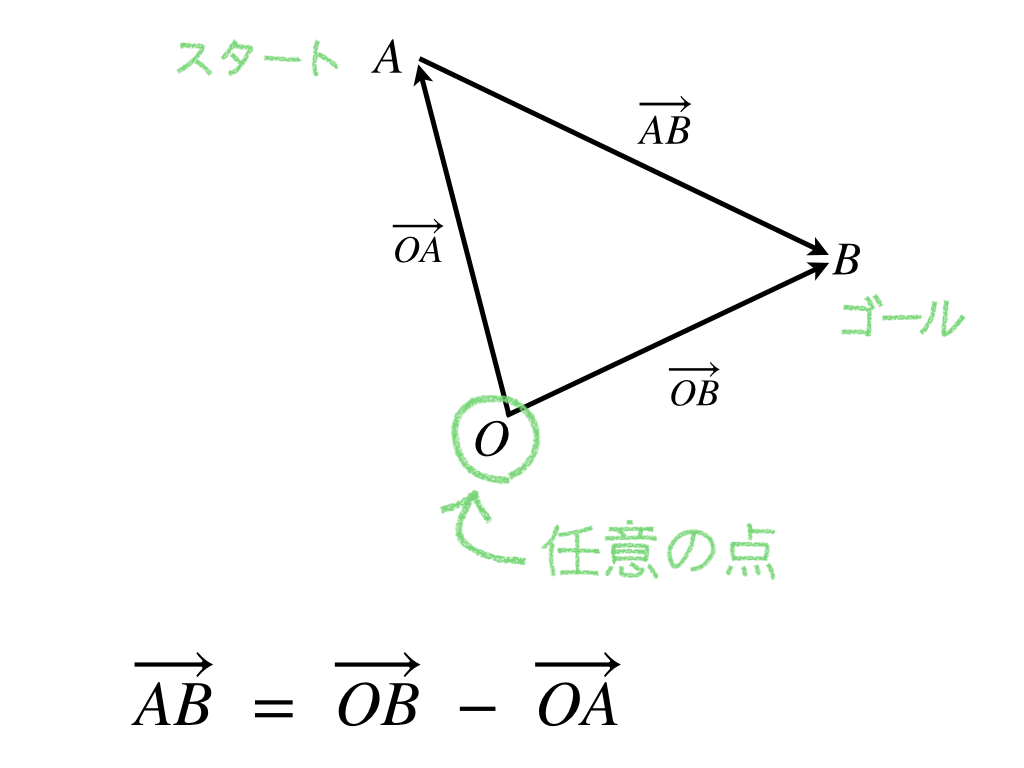
このベクトルの減法は、逆ベクトルの加法を考えることで説明できます。
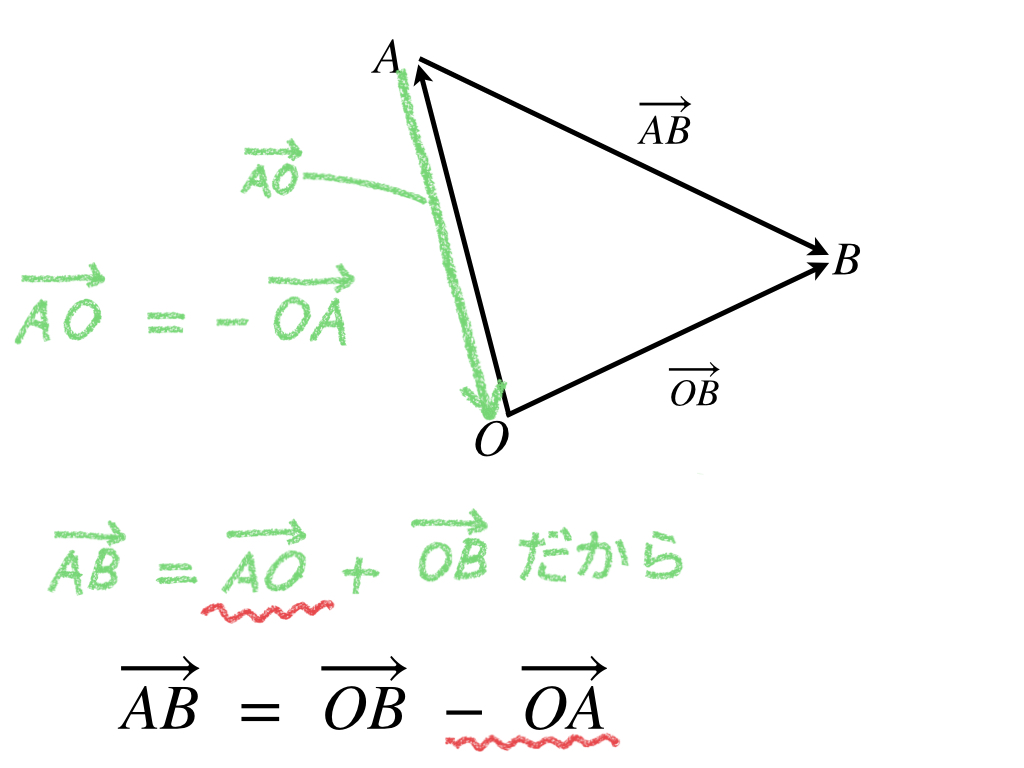
この変形は、ベクトルの計算ではよく使うものです。点Oは任意ですので計算しやすいように選びます。
ベクトルの実数倍
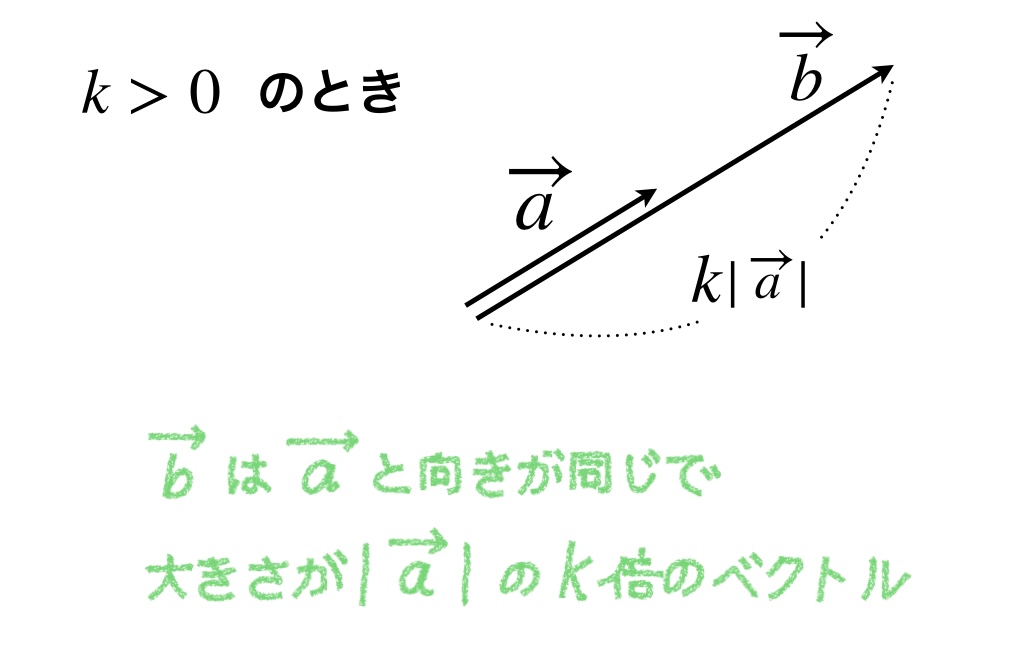
ベクトルに正の実数を掛けると、向きは変わりませんが、大きさが元のベクトルの掛けた実数倍になります。
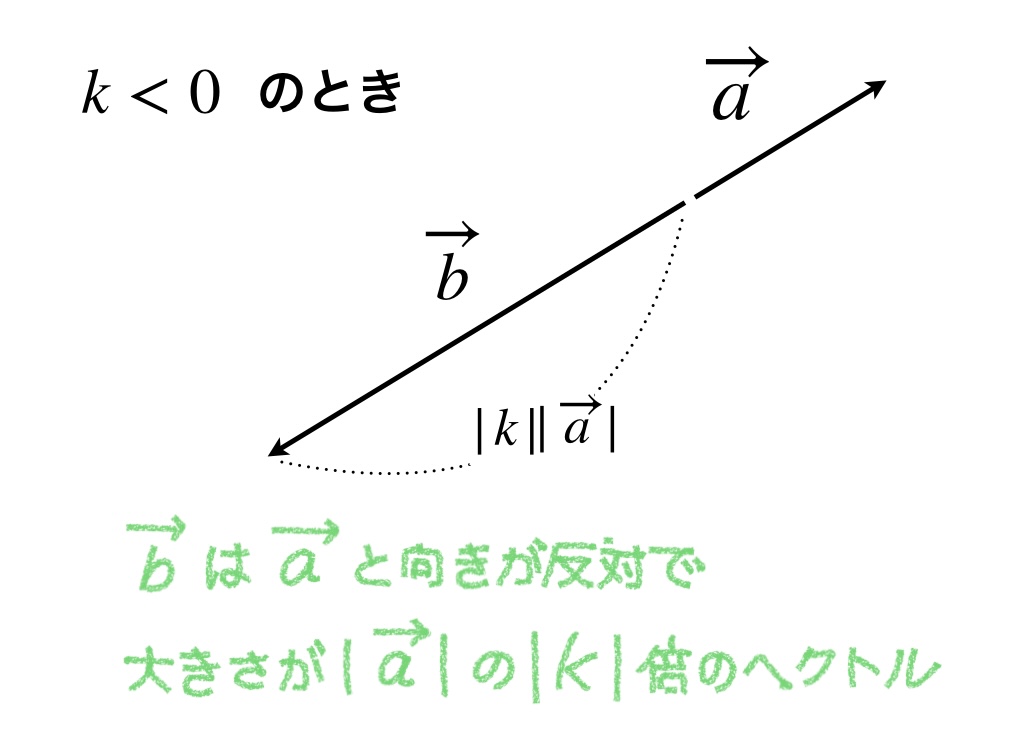
ベクトルに負の実数を掛けると、向きが反対になり、大きさが掛けた実数の絶対値倍になります。
ベクトルに0(ゼロ)を掛けると零ベクトル(ゼロベクトル)になります。
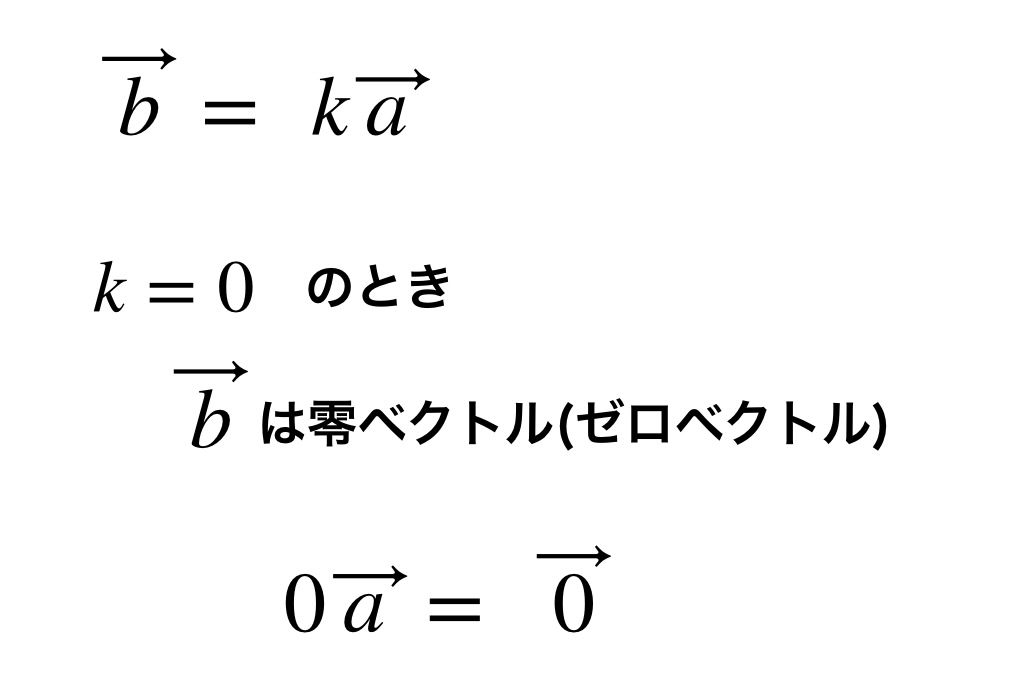
実際にベクトルの問題を解いてみよう!
ここまでの知識があれば、次のような問題が解けるようになります。早速解いてみましょう!

問題文を図にすると次のようになります。
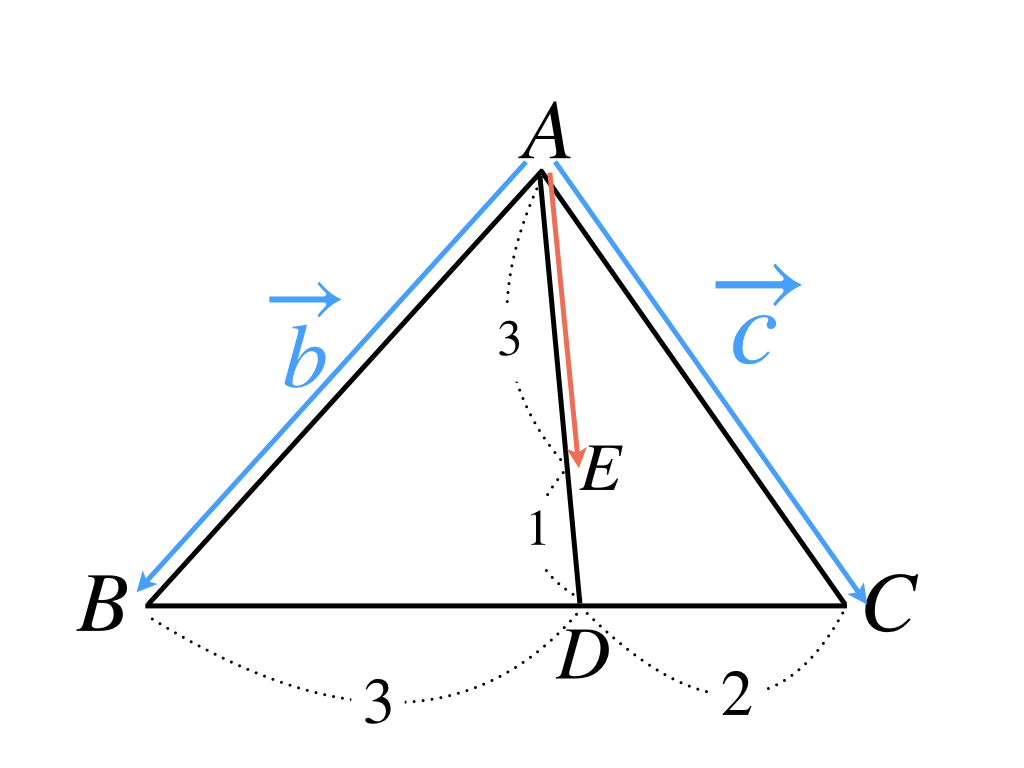
先ず最初に、ベクトルAEとベクトルADに着目して下さい。ここでは「ベクトルの実数倍」の公式を使います。

ベクトルAEがベクトルADで表されました。次にベクトルADを次のように表します。
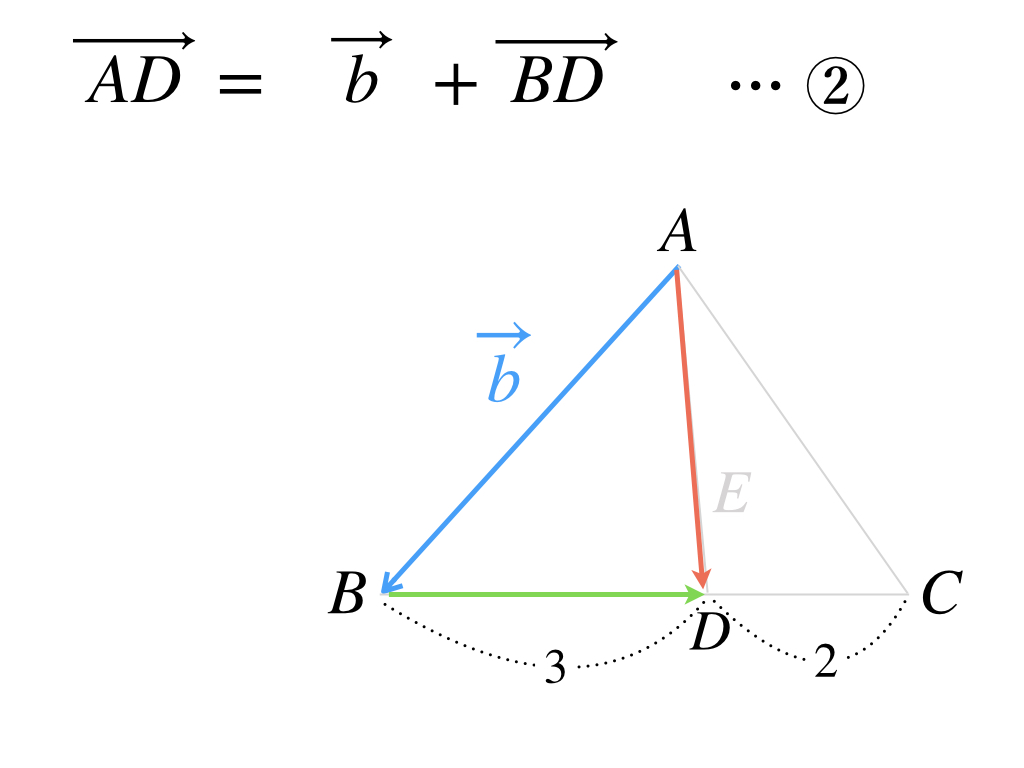
これは「ベクトルの和」の公式を使っているのが分かりますね。これで、ベクトルADがベクトル b とベクトルBDで表されました。
次にベクトルBDです。
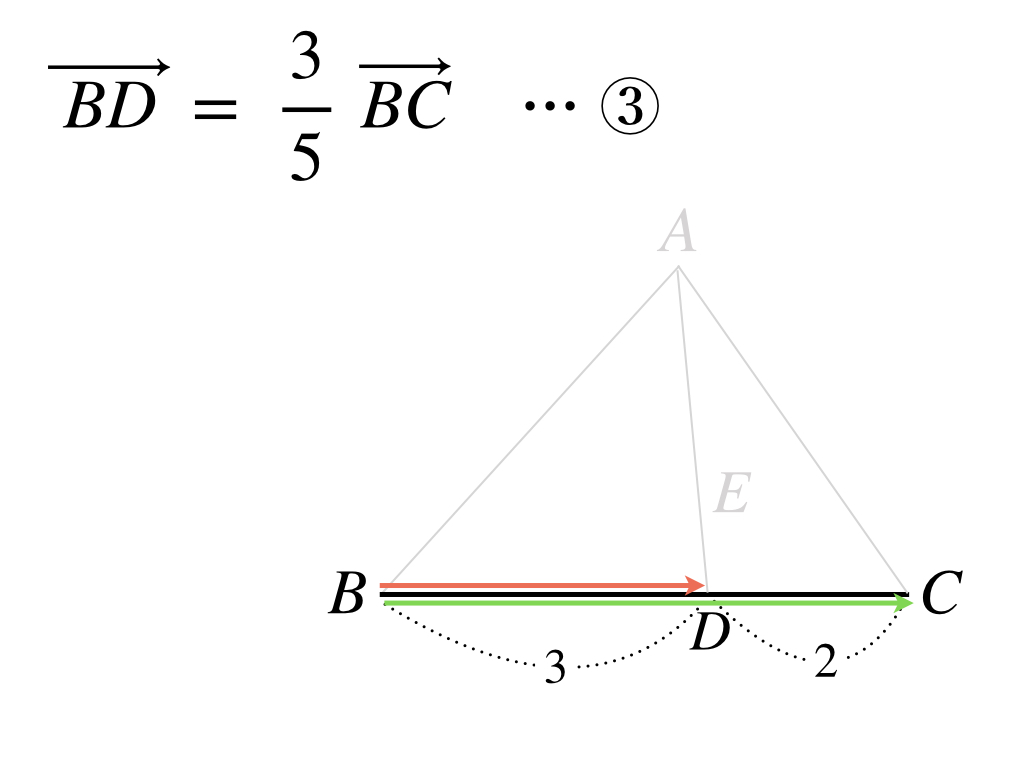
これも「ベクトルの実数倍」の公式を使っています。これでベクトルBDがベクトルBC で表されました。最後にベクトルBCを次のように表します。

これは「ベクトルの差」の公式を使っています。これでベクトルBCがベクトル b とベクトル c で表せました。ここまでの式をまとめると次のようになります。
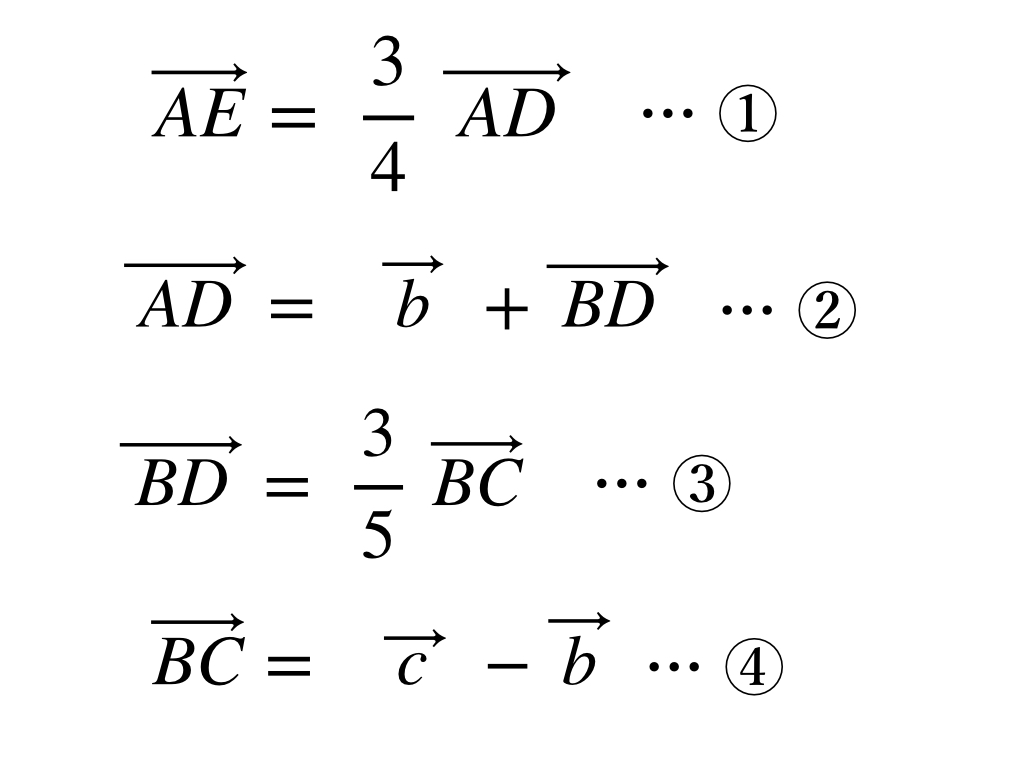
これらの式は、どのような順番で作ったのかと言うと、求めたいベクトルAEから始めて、ベクトル b とベクトル c だけになるまで分解し続けたのでした。
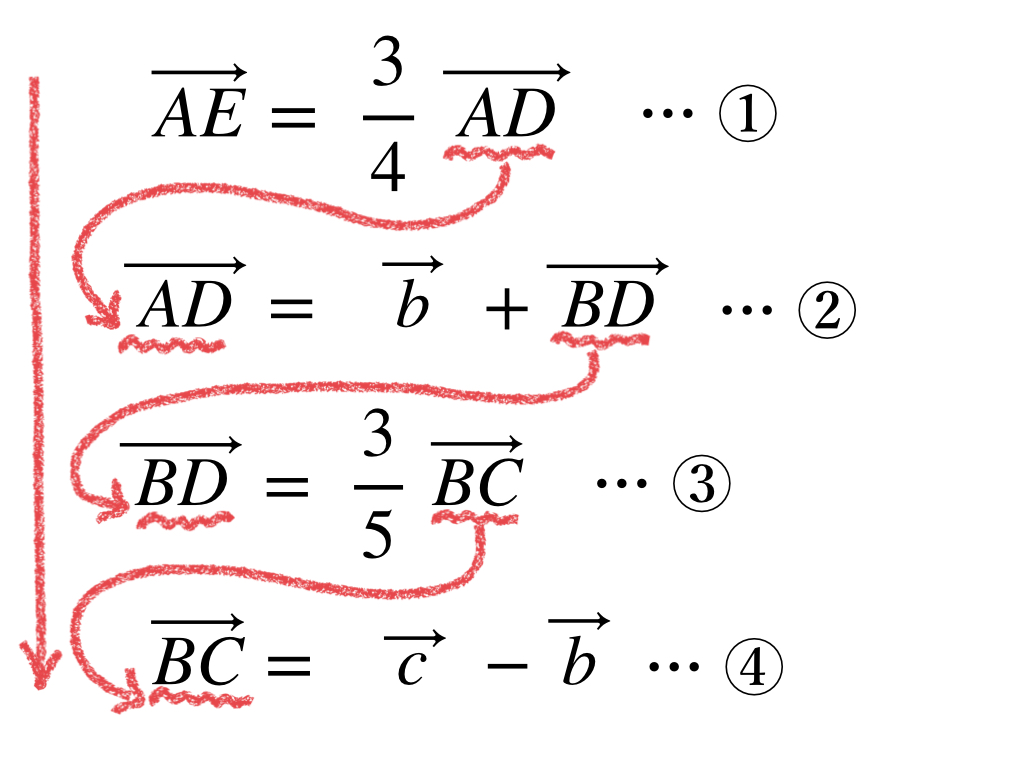
これで使う式は用意できたので、今度はこれらの式を逆方向に組み上げていきます。

では順番にやっていきましょう。④ の式を ③ の式に代入します。できた式が ③’ です。
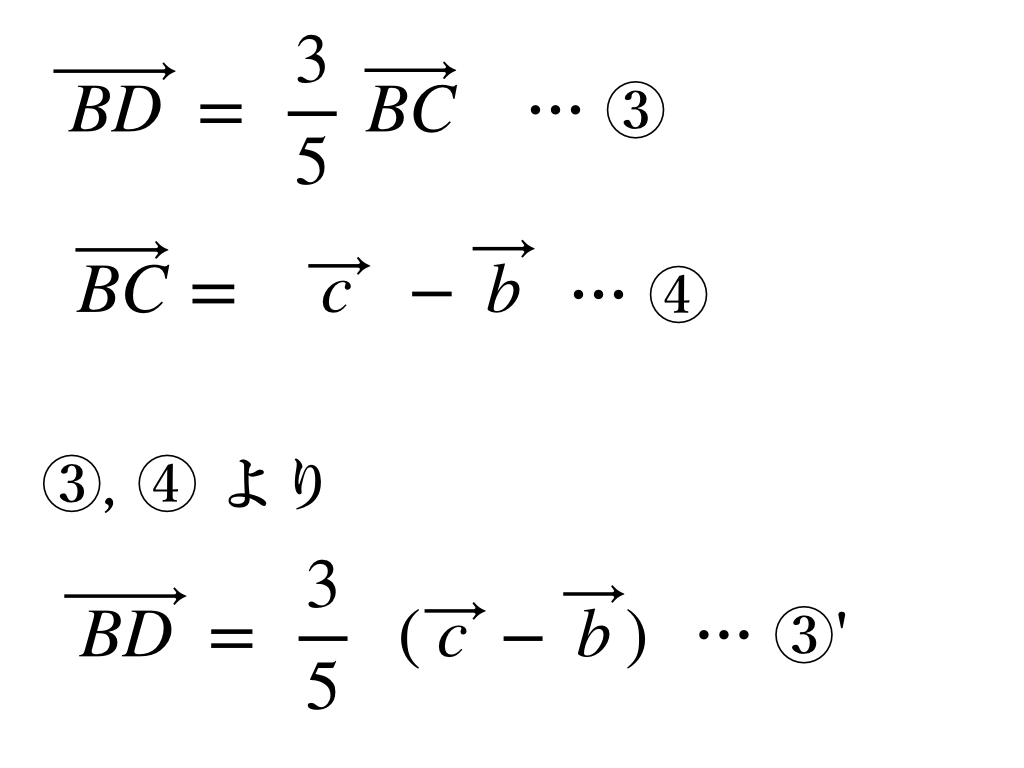
次に③’ の式を② に代入します。できた式が②’ です。
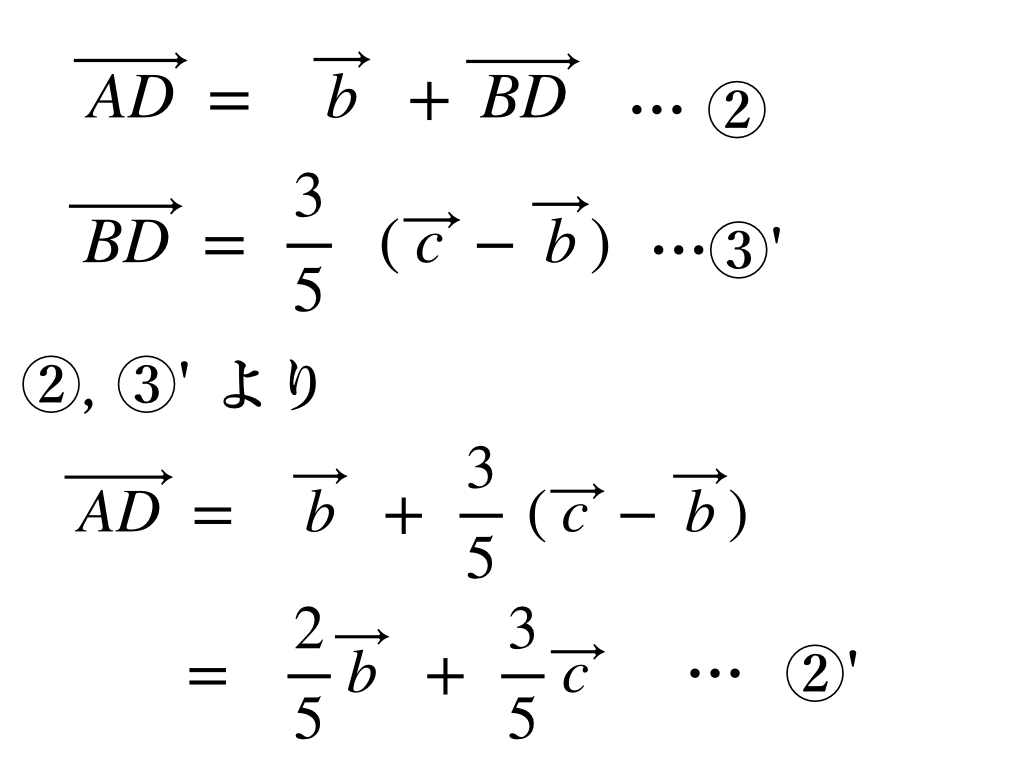
最後に②’ の式を① の式に代入すれば、求める答えが得られます。
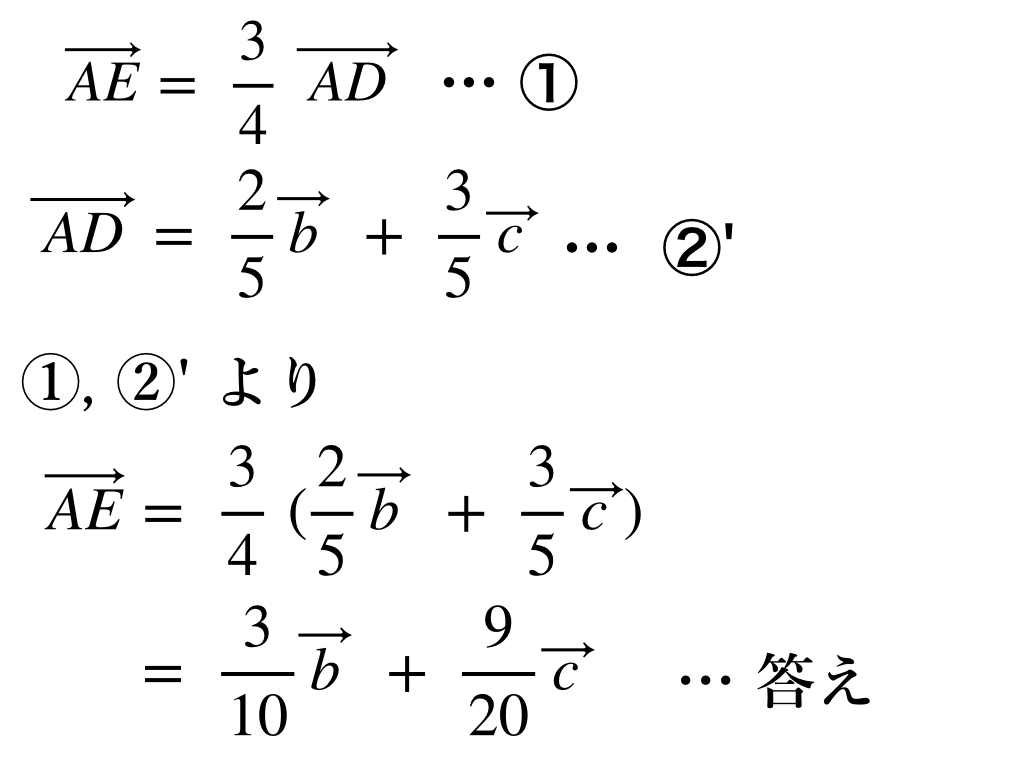
このように公式通りに式を作っていけば、あとはそれらの式を計算することによって答えが得られます。
まとめ
ベクトルの醍醐味は、図形問題を計算で解けてしまえる点にあります。公式どおりに式さえ作ってしまえば、あとは計算です。
ベクトルを、どのように活用するのか、理解してもらえたら嬉しいです。
 家庭教師の想い
家庭教師の想い 

