【シグマの計算】苦手になるポイントを徹底解説！

シグマの計算で失敗するポイントは決まっています。それは分数と因数分解の処理です。またシグマの計算と等差数列の和や等比数列の和の計算との関係をはっきりさせれば、シグマの計算が得意になります。

【スタディサプリ】動画授業で苦手を克服

数列の和の公式

まずは公式から確認しましょう。

1️⃣は意外と忘れがちです。しっかりチェックしましょう。

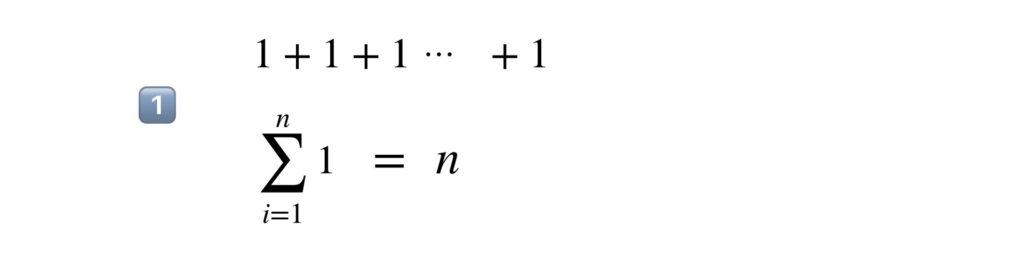
2️⃣は、初項１、公差１、項数 n の等差数列の和を意味しています。

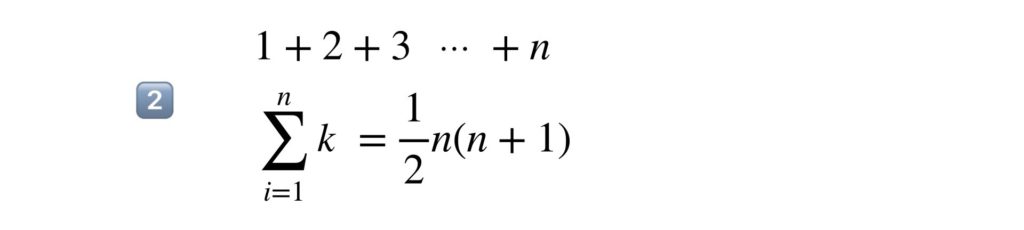
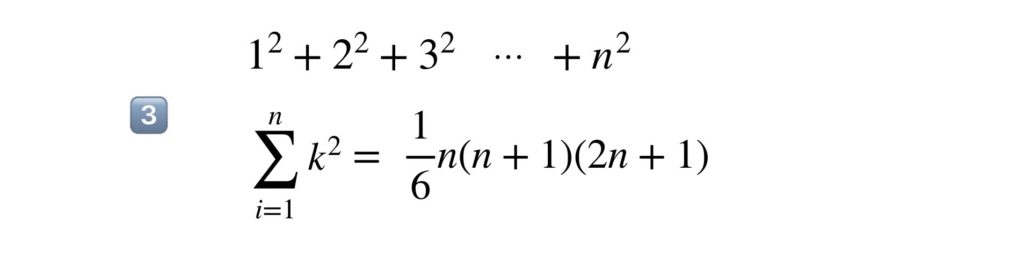
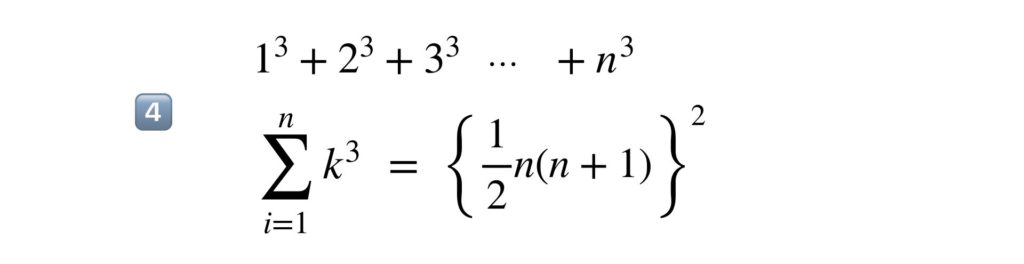
そしてもうひとつ、使い方で悩んでしまうのは次の5️⃣の公式ですね。これは初項１、公比 r 、項数 n の等比数列の和を意味しています。この公式の使い方にも間違いやすいポイントがありますので後ほど詳しく解説します。

次のふたつの性質も大切です。シグマの計算でもっとも大切な性質だと言っていいかもしれません。このふたつの性質によって複雑な数列の和が計算を進めるだけで求められるようになります。

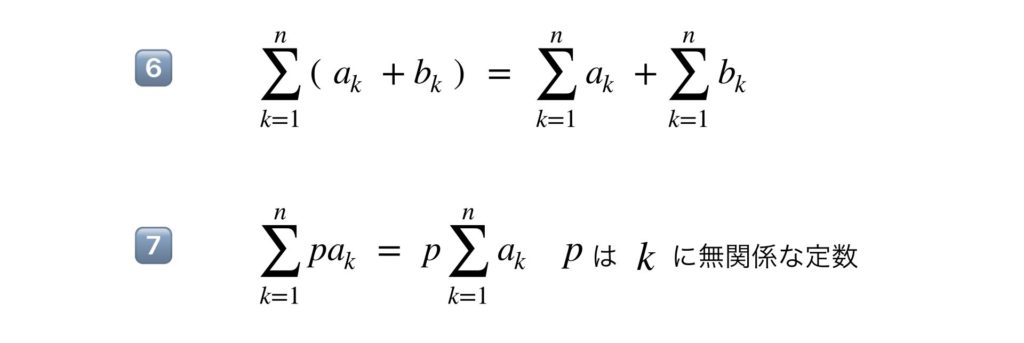
シグマの計算を含む問題を解いてみよう

では、実際に問題を解いてみましょう。次の【問】を見てください。シグマの計算が有効な問題です。

各項を並べた数列は、最後の一般項が示すとおり、かなり複雑なものですが、その和はシグマの公式で計算すれば求められます。ここがシグマの計算のすごいところです。

先ず、この数列の和をシグマで表します。 この問題では数列の一般項が文字 n で与えられています。その n を k に変えてシグマの中に入れればいいのです。そして公式6️⃣を使います。

つぎに公式3️⃣と4️⃣を使ってシグマの式を n の式に変えます。

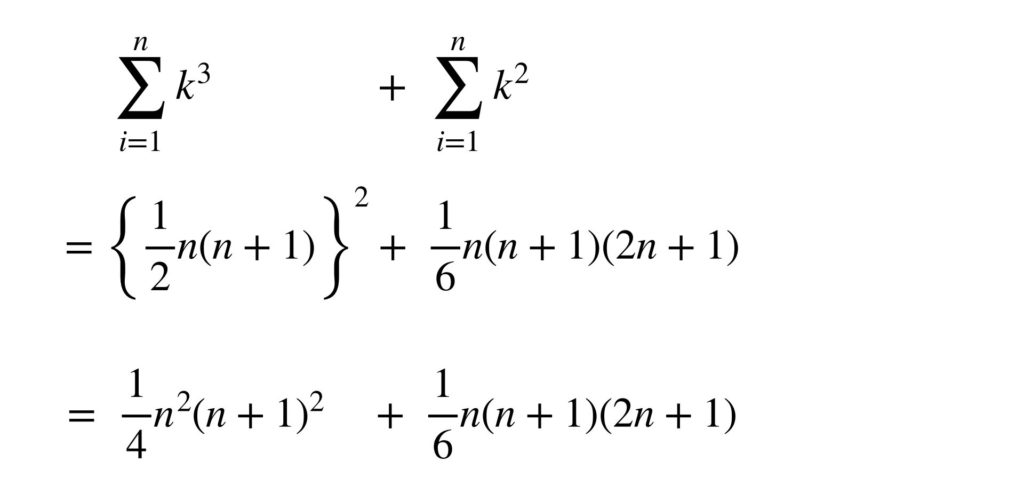
ここまでは問題なくできたのではないでしょうか。でもシグマの計算が苦手なひとはここから先で手こずります。決して式を展開してはいけませんよ。このまま因数分解を考えていくのです。つまり共通因数をくくり出します。

でも困ってしまうのは分数の扱いです。それは次のようにしてください。分母を同じ数にするのです。

ここまで来たら、もうできたようなものですが、この問題ではまだ続きがあります。２次式の部分の因数分解を考えましょう。

これで出来上がりです。

シグマの計算では、公式を使う場面では問題は少ないのですが、式をまとめていくとき失敗が生じやすいのです。

シグマの式の内容を理解する

場合によってはシグマなんて使わずに計算した方が速く正確に答えが得られるときがあります。

シグマの式が意味している内容を読み取れば、効率よく、かつ正しく計算できるようになります。

シグマの中が１次式のとき

次の計算はシグマの中が k の１次式の場合の計算です。シグマの公式を使って実際に計算すると次のようになります。公式1️⃣と2️⃣、性質6️⃣、7️⃣を使っています。

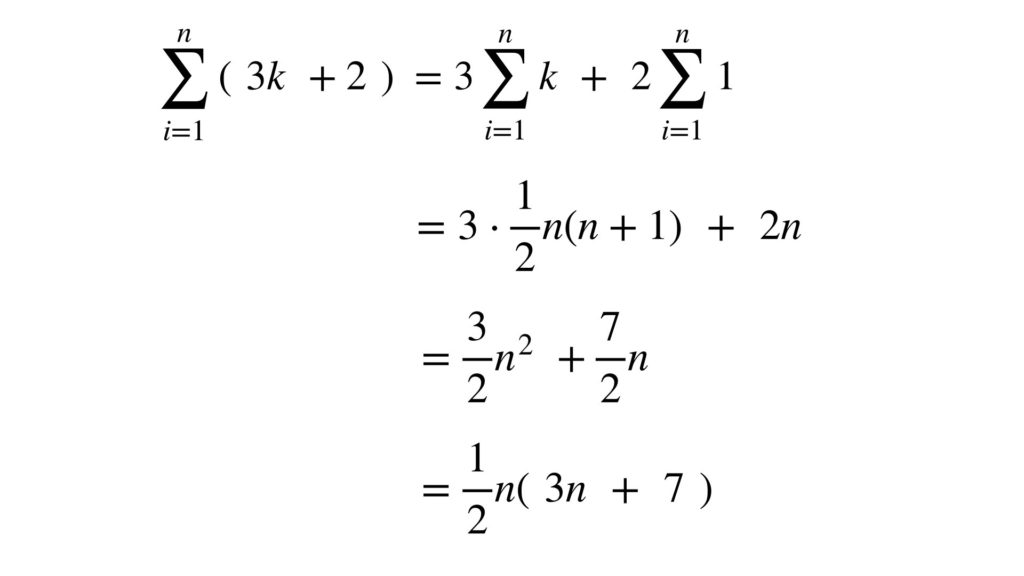
簡単のようで意外とめんどくさいですね。

数列の一般項が n の１次式の場合、その数列は等差数列を意味しています。初項は n = 1 を代入すれば求まります。公差は n の係数に一致します。末項は n 番目の項です。

ですからシグマの中が k の１次式であれば、それは等差数列の和を意味するのです。この場合、次のように等差数列の和の公式を使った方がシグマの計算より簡単です。すなわち初項と末項を足して２で割り、それに項数を掛けるのです。

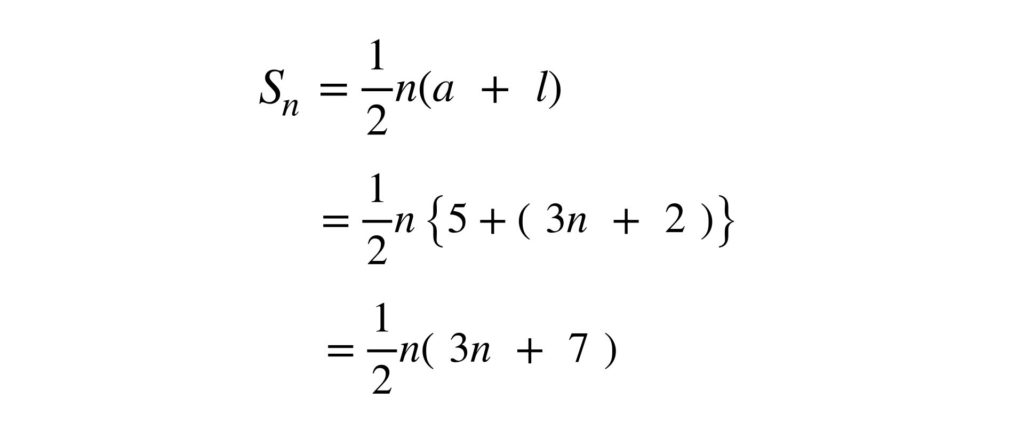
シグマの中が１次式の場合、等差数列の和の公式を思い出しましょう。

シグマの中が累乗になっているとき

シグマの式に累乗が入っている場合、計算に注意が必要です。公式5️⃣をもう一度確認しましょう。

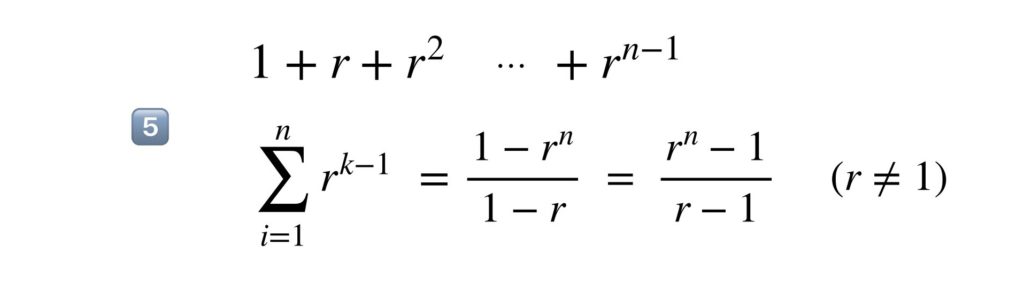
これはどこかで見たように思いましたか？そうですね、等差数列の和の公式です。等差数列の和の公式は次のようなものでした。初項が a 、公比が r 、項数が n です。

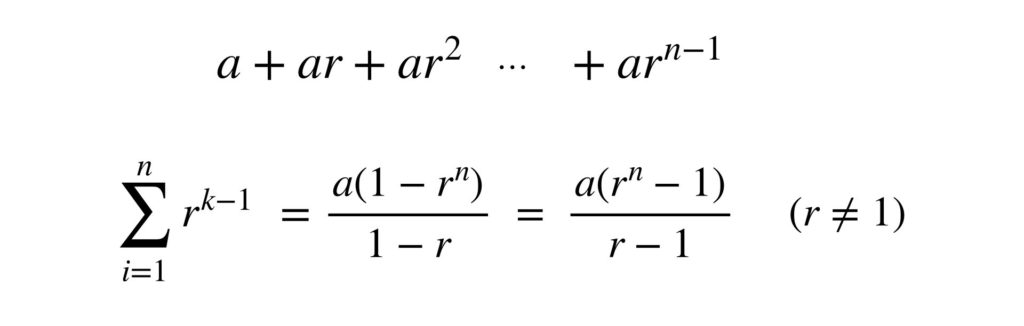
で、5️⃣の公式を使うとき、ミスを犯しやすいのは次の赤で囲った部分です。

どのように間違えるかと言うと…

どこで間違えたか分かりましたか？5️⃣の公式と見比べましょう。

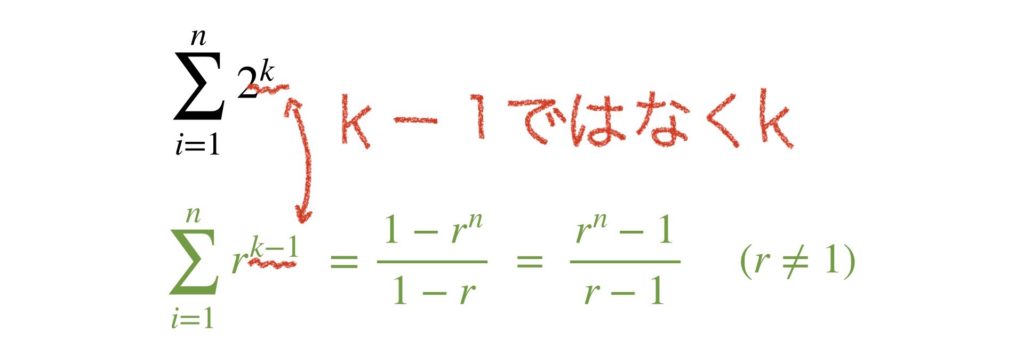
公式のシグマの中は k-1 乗になっていますね。公式を使うなら、ここを k-1 にする必要があります。次のようにしましょう。

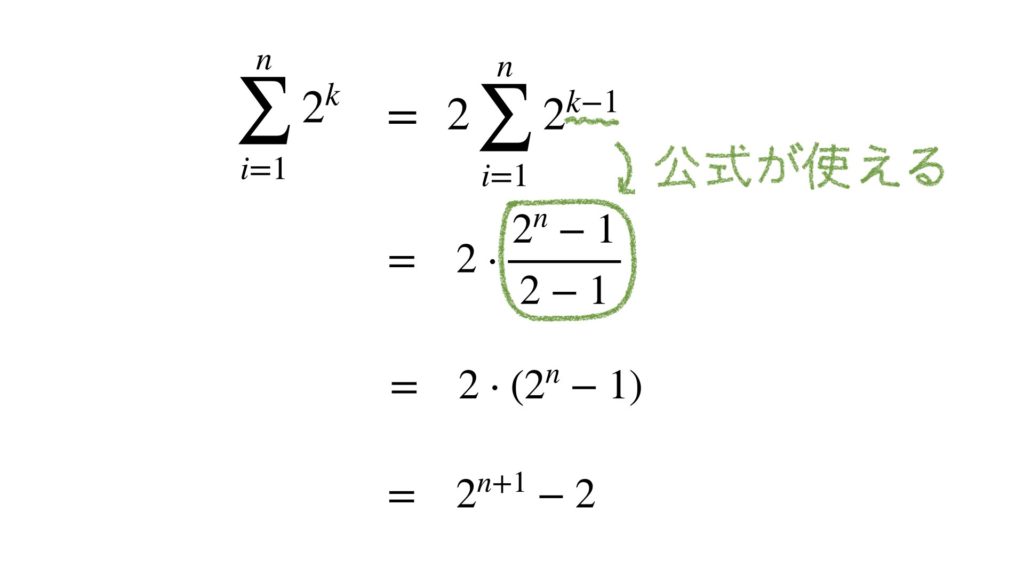
しかし、これだったら初項が２、公比が２、項数 n の等比数列の和と考えた方がいいのです。

公式を使って、ただ計算をすると自分が意識していないところでミスしてしまいます。ちゃんとシグマの式が意味している内容を掴んだ上で計算した方がミスを減らせます。

次の計算も考えてみてください。

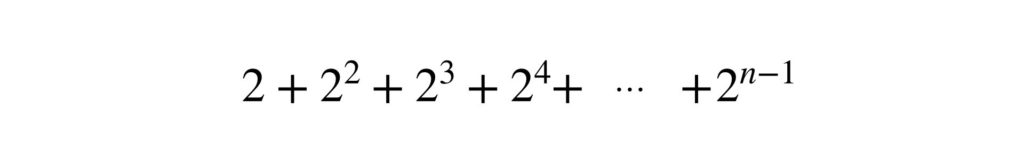
これも初項２、公比２、項数 n – 1 の等比数列の和と考えられます。

このようにシグマの計算は、ただ公式を使って計算するだけではなく、シグマの式が意味している内容をしっかり掴んで計算するべきなのです。

まとめ

シグマの計算で大切なポイントをまとめました。

以上の点に注意してシグマの計算を進めましょう。