ベクトル方程式とは、どのようなものでしょうか?
直線や円のベクトル方程式は図形の方程式の一種ですが、では図形の方程式とは何でしょうか?
見慣れたもので確認しましょう。次の方程式を満たす点 $(x, y)$ の全体からできる図形は直線ですね。
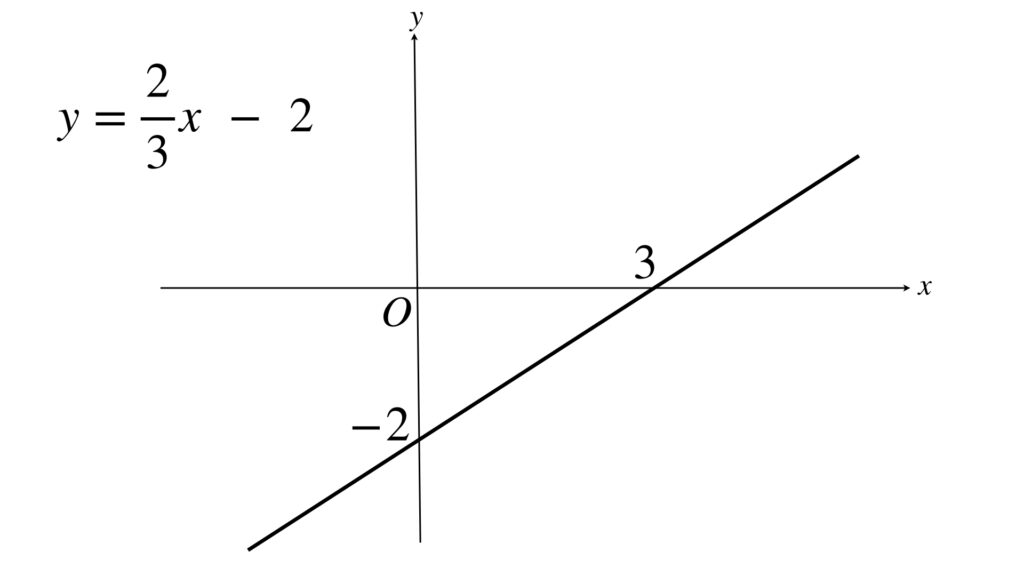
これは $x$ の値をひとつ決めると $y$ がひとつ決まり、それらの点の全体の集合が直線になるこということです。
これが座標を使った直線の図形の方程式です。いわゆる直線の方程式といわれるものですね。
つまり点が存在できる範囲を方程式で限定させると、その点の全体の集合で図形を表せるというわけです。
点の位置は、座標ばかりでなくベクトルを使っても表せます。これが位置ベクトルです。
ですから点が存在できる場所の決まりをベクトルを使って表すのがベクトル方程式なのです。
ベクトル方程式を知るには先ず位置ベクトルをちゃんと理解しなければいけません。
では位置ベクトルの復習から始めましょう。
目次
位置ベクトル
「あなたの家はどこにありますか?」
そう聞かれたら、例えば次のように答えられます。
「◯◯公園から北東に300メートルだよ」
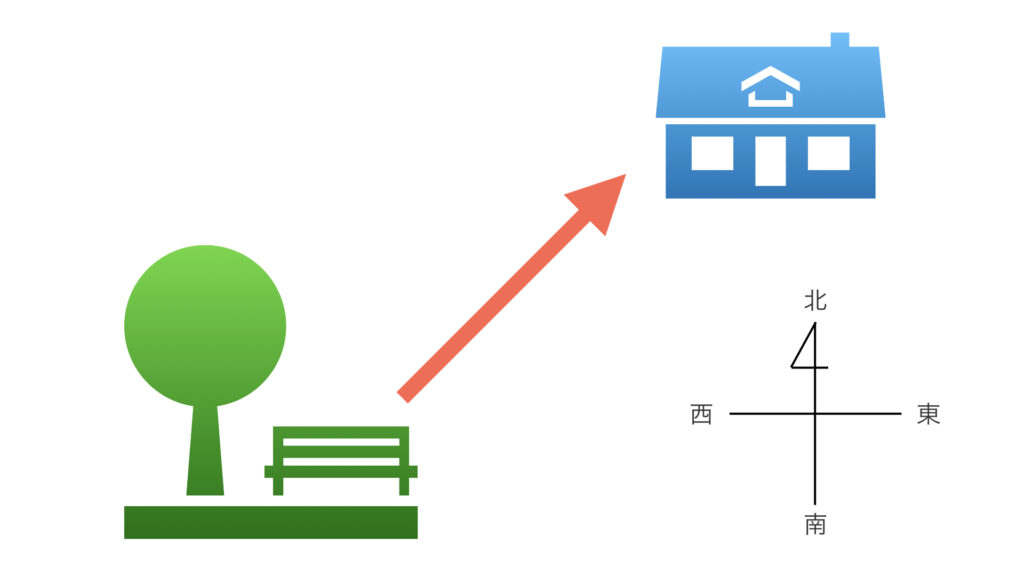
このように基準点から方向と距離を示せばひとつの地点を決定できます。
先程の例なら公園が基準点です。
平面上で任意の点の位置は、基準点である点 $O$ を固定して考えれば、ベクトル $\overrightarrow{p}=\overrightarrow{OP}$ によって定められます。このベクトルが位置ベクトルです。
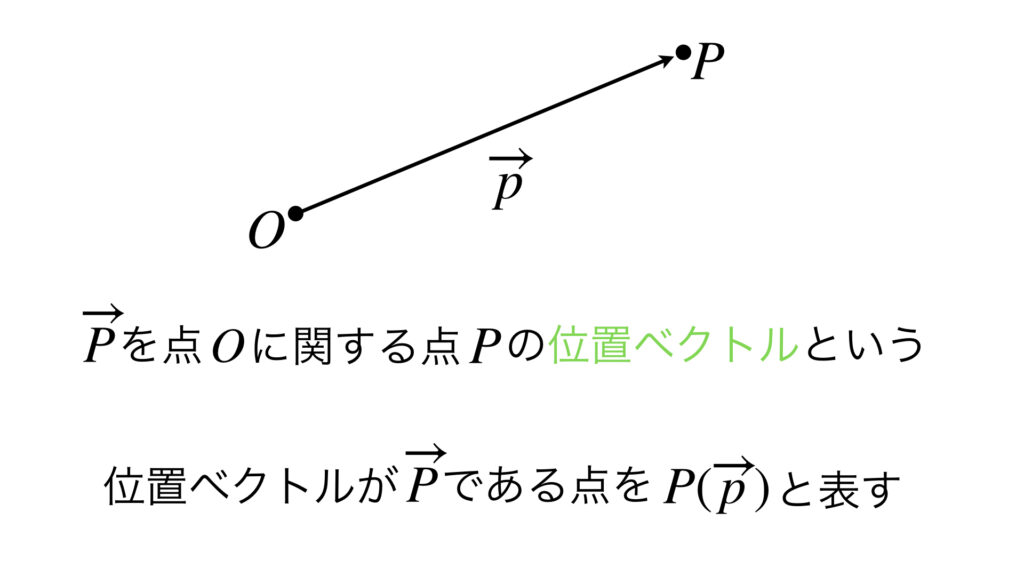
基準点である点 $O$ は平面上のどこに置いても構いません。先程の例なら基準点を変えて自分の家を「◯◯病院から西に200メートルだよ」と答えられます。
さて、位置ベクトル $\overrightarrow{p}=\overrightarrow{OP}$ で示された点 $P$ に何の条件も与えなければ、点 $P$ は自由気ままに動いてしまいます。
この点 $P$ が特定の図を描くように条件を与えましょう。
直線のベクトル方程式
直線と方向ベクトル
では動点 $P$ に直線を描くように条件を与えます。
直線を描く方法のひとつは、平面上に定点を取り、そこから直線が伸びていく方向を決めれるやり方です。
これは、自分の家から方角を定めて、ひたすら真っ直ぐに歩けば、自分の位置の軌跡が直線(この場合は半直線ですが)を描くことと同じです。

点の位置は位置ベクトルで表せますが、そのためには基準点を定める必要がありましたね。今回は公園を基準点としましょう。
この公園から見て人の位置はどのように表せるでしょうか。

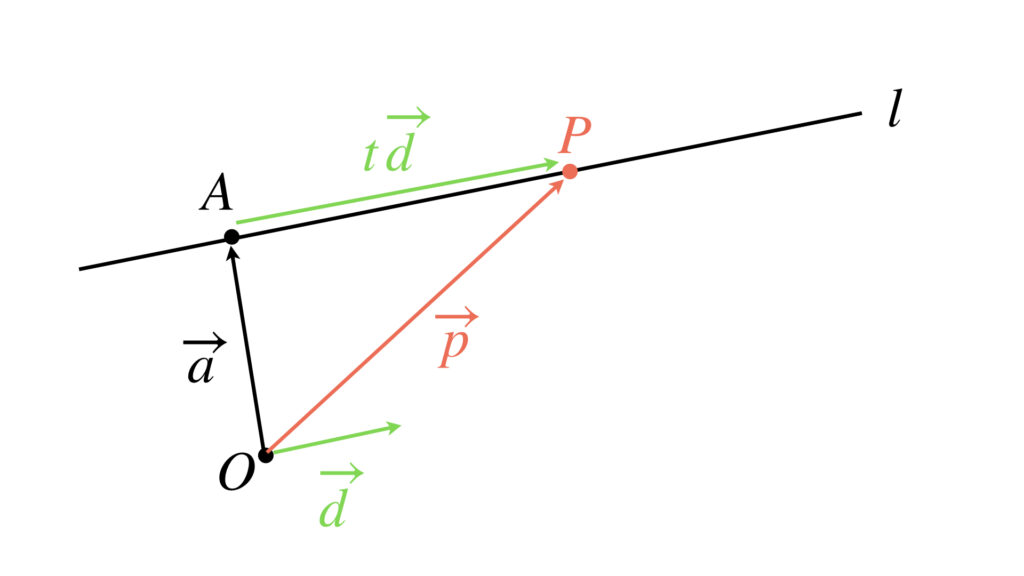
家が定点 $A$ で人が動点 $P$ だと思ってください。
最初に定点 $A$ の位置を決めます。これは位置ベクトル $\overrightarrow{a}=\overrightarrow{OA}$ によって定められます。
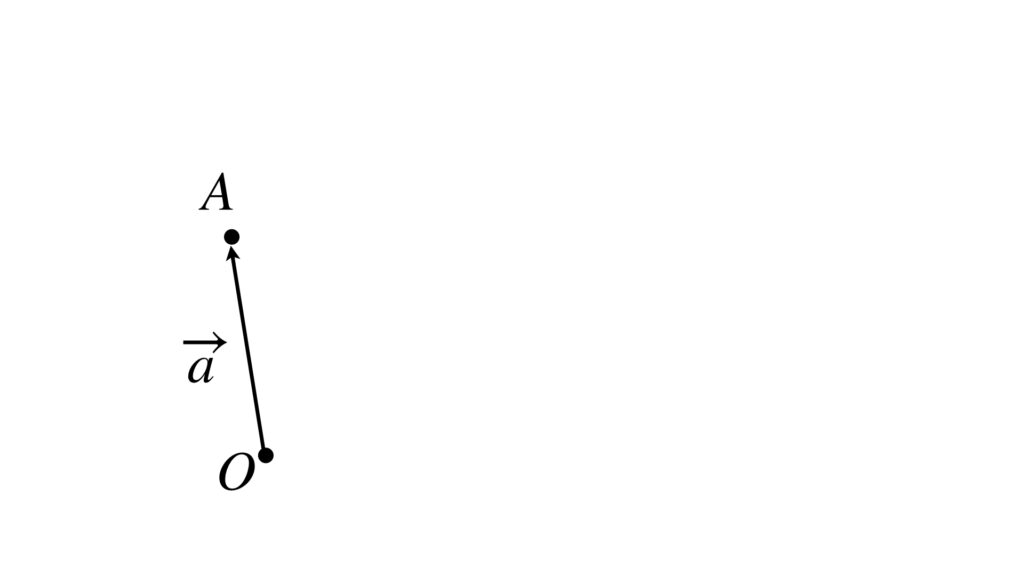
この点 $A$ を通って、ある方向に伸びていく直線 $l$ を考えましょう。
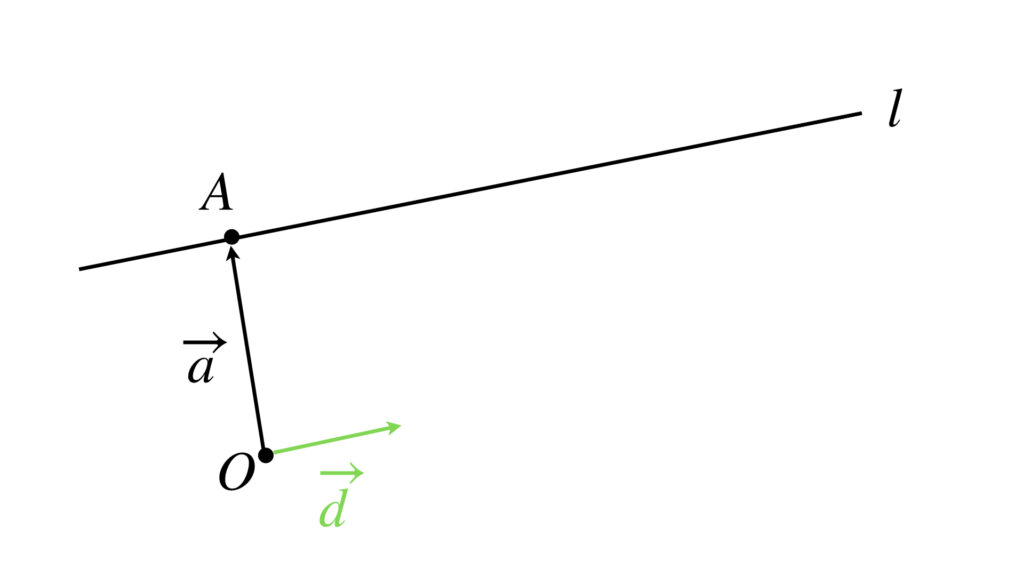
この方向を与えるのが方向ベクトルです。図では $\overrightarrow{d}$ がそれです。方向さえ与えてくれればいいので、方向ベクトルの大きさは $0$ でなければいくつでも構いません。
では動点 $P$ がこの直線上でしか動けないようにベクトル方程式で条件を与えましょう。
点 $P$ の位置ベクトルを $\overrightarrow{p}$ とします。
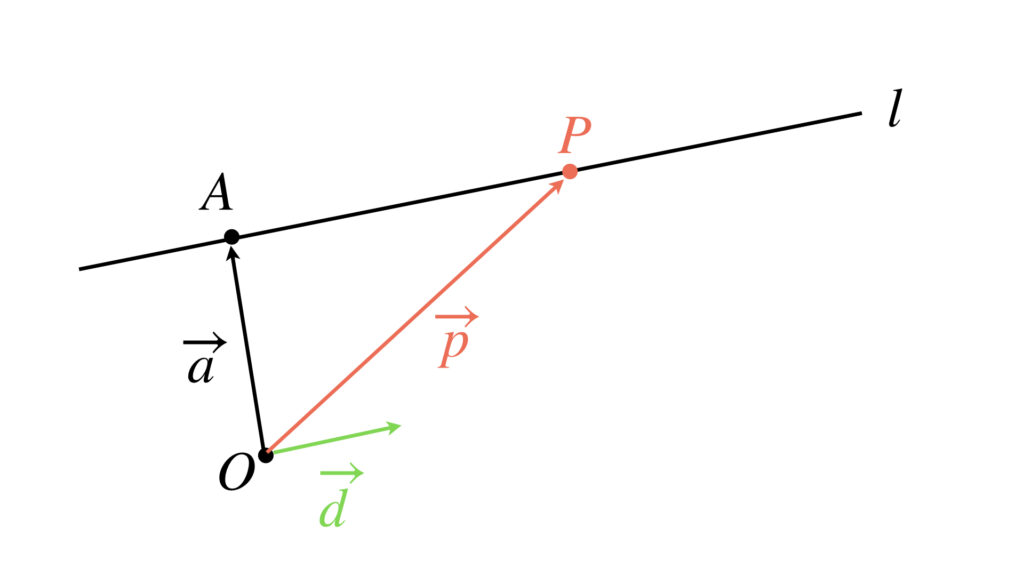
点 $P$ が直線 $l$ 上にあるなら、次の条件が成り立ちます。

$\overrightarrow{AP}=\overrightarrow{0}$ とあるのは、点 $P$ が点 $A$ と一致してもいいからです。
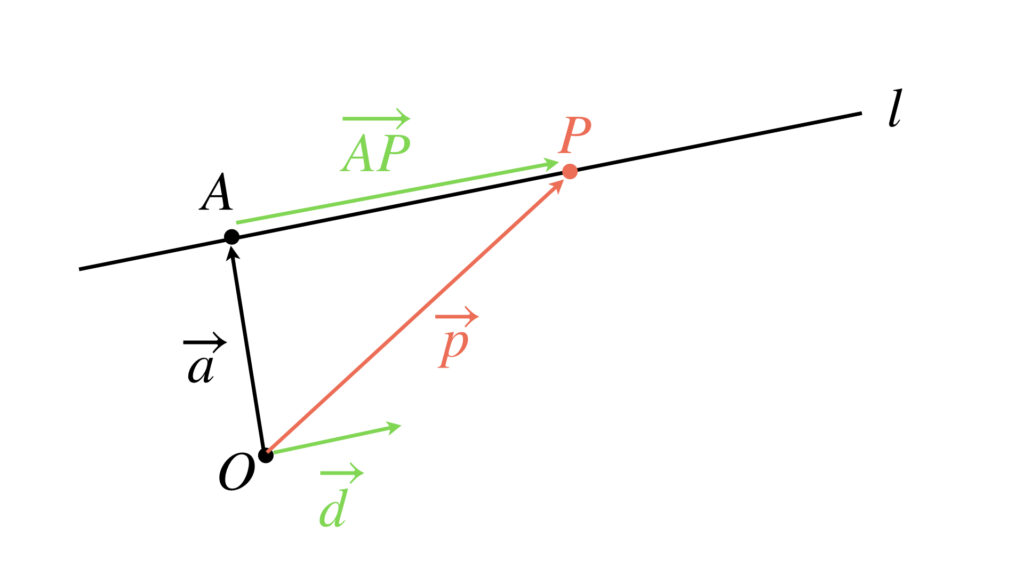
動点 $P$ が直線 $l$ 上にあることをベクトル方程式で表したいのですが、それにはベクトルの平行条件を使います。
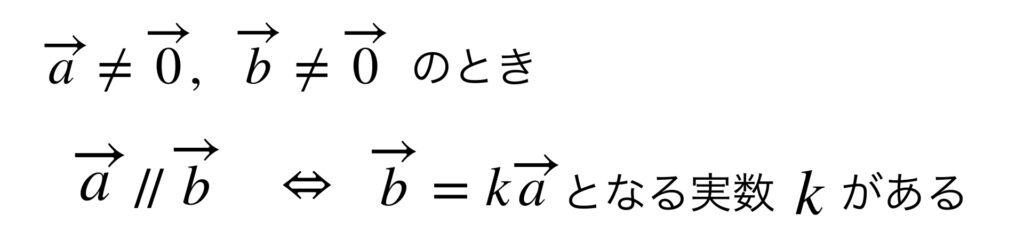
$\overrightarrow{AP}$ と $\overrightarrow{d}$ が平行であるのは次の式で実数 $t$ があることと同値です。
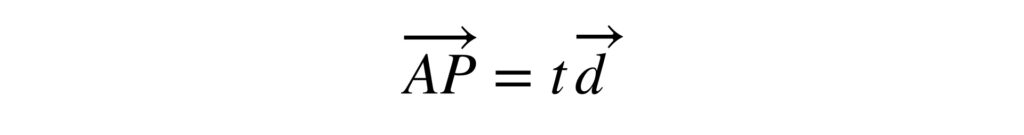
$\overrightarrow{AP}$ を $t\overrightarrow{d}$ に置き換えます。
これより次の式が成り立ちます。
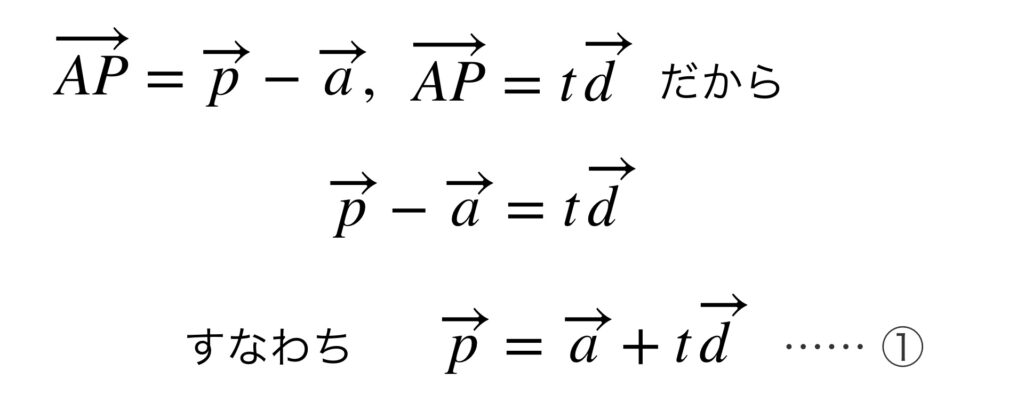
①の式で $t$ がすべての実数値をとって変化するとき、点 $P$ は、直線 $l$ 上のすべて点を示しています。すなわち点 $P$ は直線 $l$ 上でしか動けません。
すなわち①の方程式は点 $A$ を通り、$t\overrightarrow{d}$ で示された方向に伸びていく直線を表しているのです。
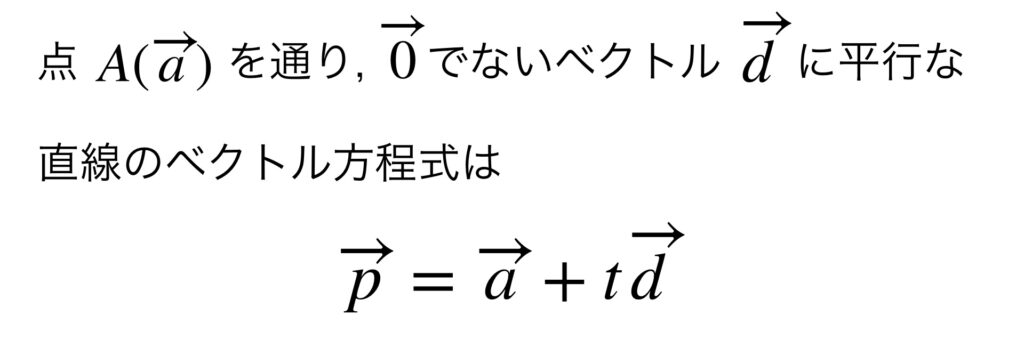
①の式を直線 $l$ のベクトル方程式といい、 $t$ を媒介変数といいます。
成分表示による方向ベクトルを使った直線のベクトル方程式
ベクトルは成分でも表すことができますね。次の図のように点 $O$ を座標平面の原点と考えます。
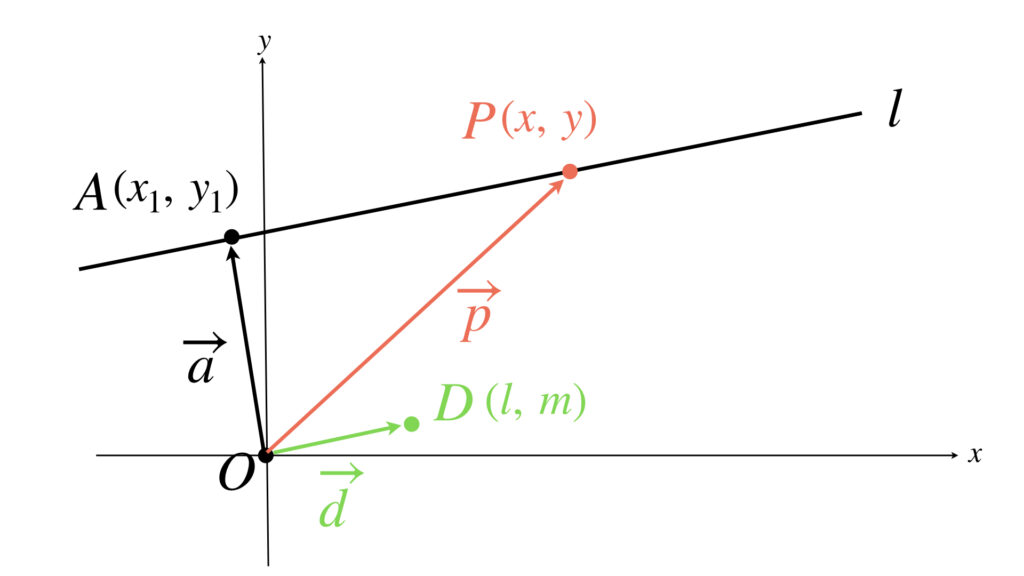
すると、それぞれのベクトルは次のように成分で表せます。
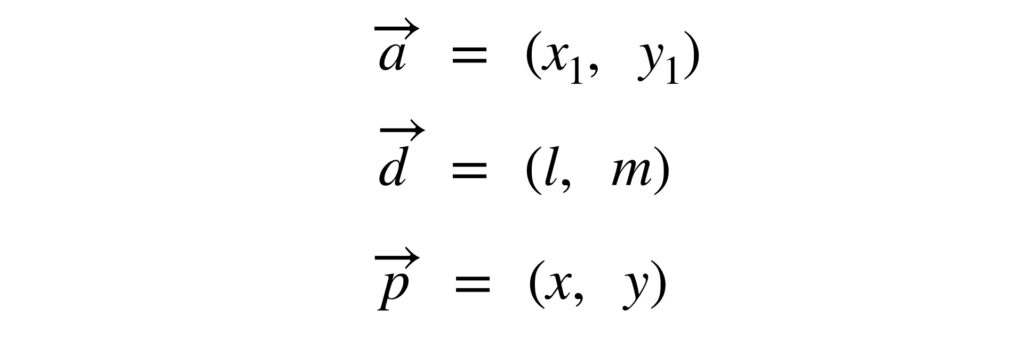
これを①に代入します。
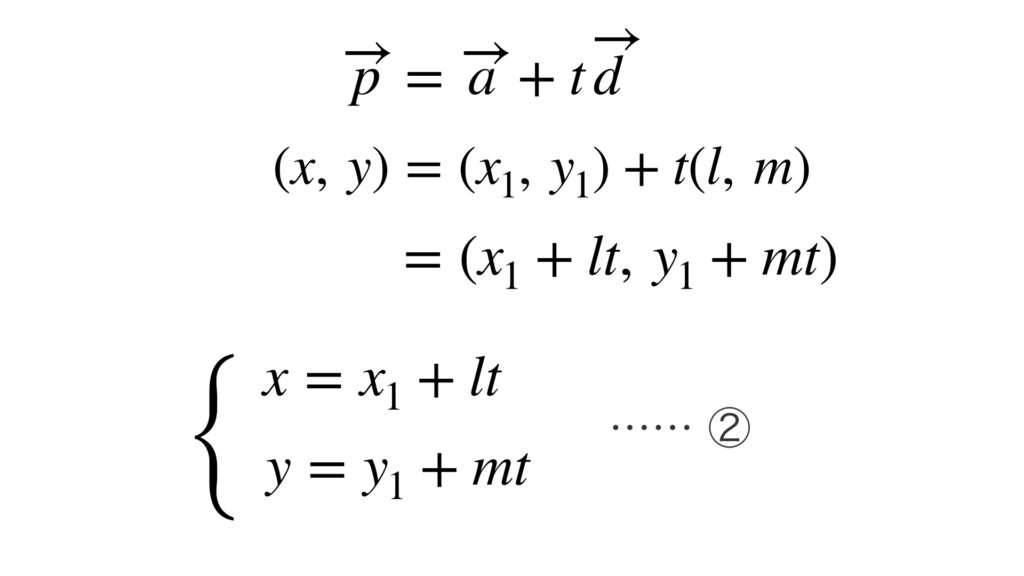
②の式を直線 $l$ の媒介変数表示といいます。
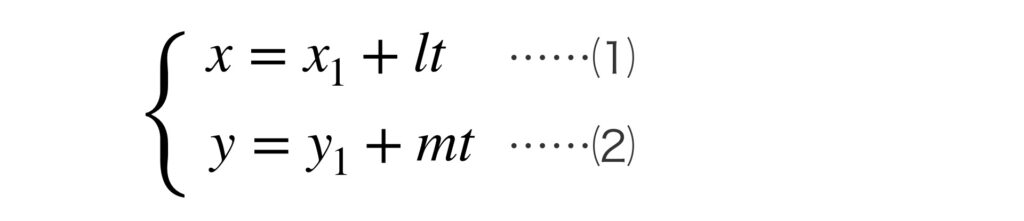
②の式から $t$ を消去してみましょう。
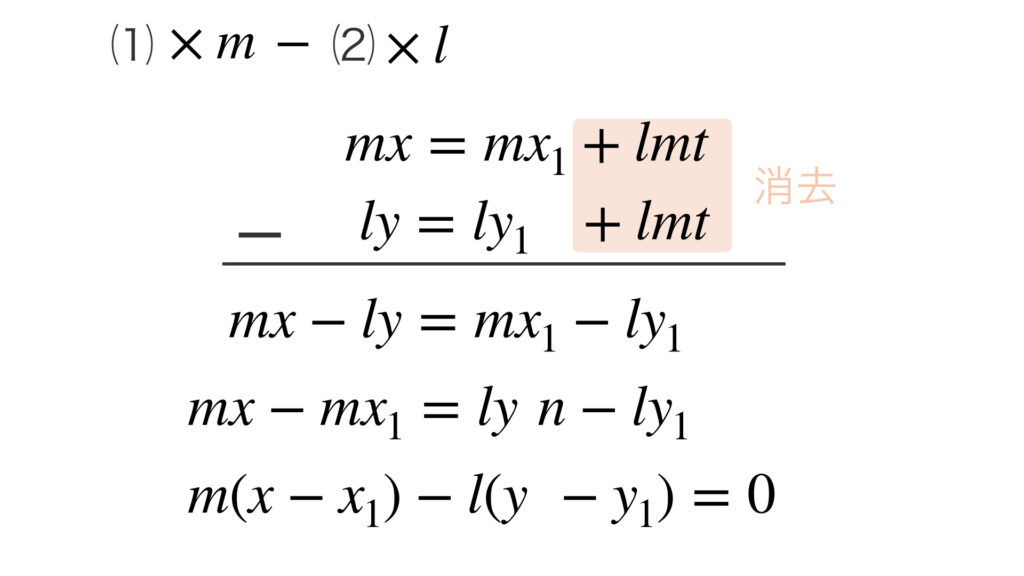
よって次のことが成り立ちます。

異なる2点を通る直線のベクトル方程式
平面上で2点を定めれば、その2点を通る直線を決定できます。
先程の例では、自分の家と病院を通る直線上を歩くようにすれば、人の軌跡は特定の直線を描くことになります。
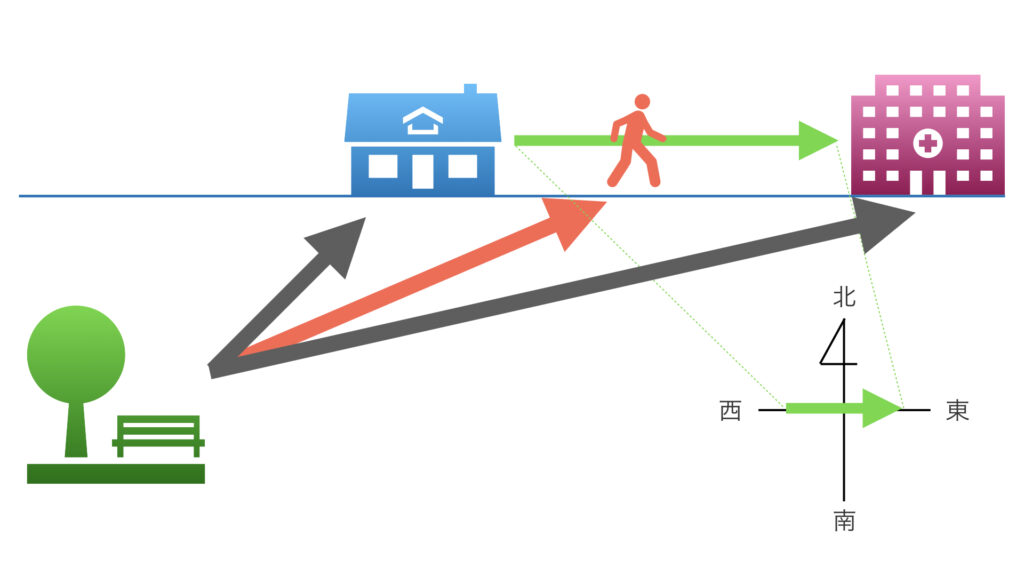
家が定点 $A$ 、病院が定点 $B$ で、人が動点 $P$ だと思ってください。
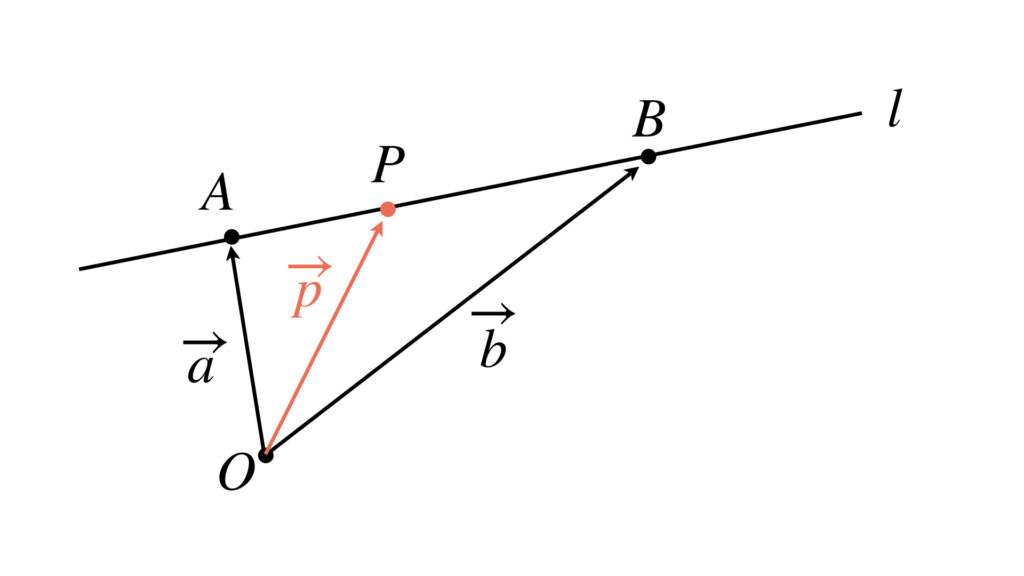
2点 $A$ と $B$ を通る直線は、ベクトル$\overrightarrow{AB}$ に平行な直線と考えても構いません。すなわちベクトル$\overrightarrow{AB}$ を先程の方向ベクトルと考えてもいいのです。
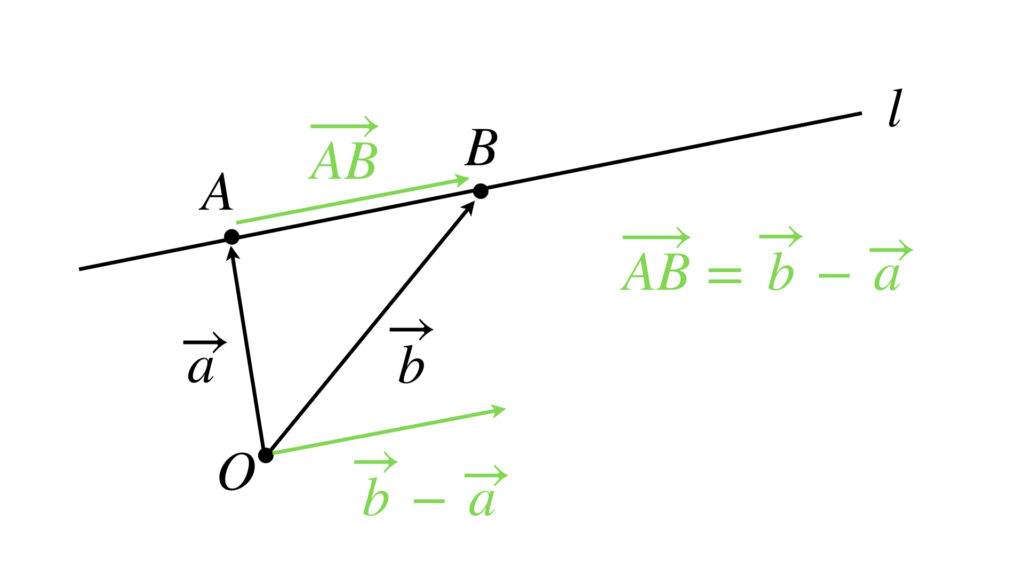
方向ベクトル $\overrightarrow{d}$ を使って表した直線のベクトル方程式は次のようなものでした。
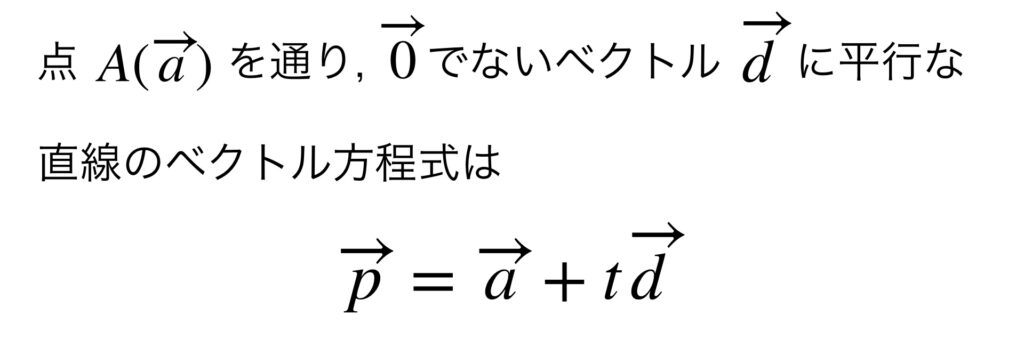
この式の $\overrightarrow{d}$ を $\overrightarrow{b}-\overrightarrow{a}$ に置き換えましょう。
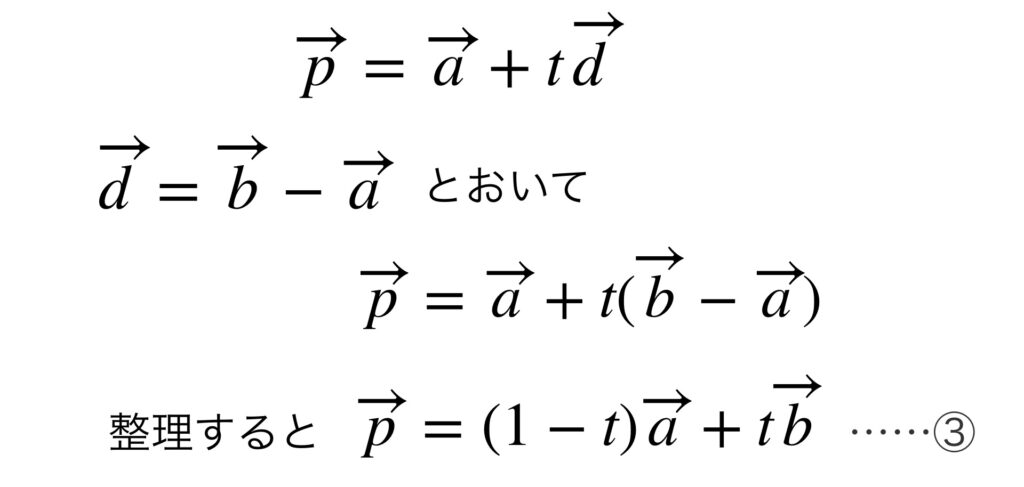
③の方程式において、$1-t=s$ とおくと、次の式の形になります。
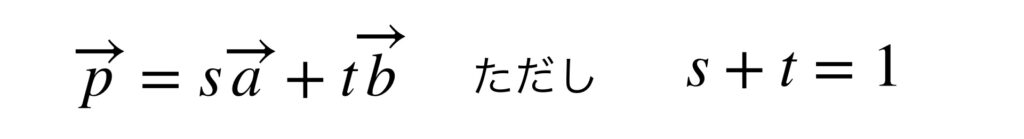
これらをまとめると次のようになります。

この式で $t$ 、または $t$ と $s$ がすべての実数値をとって変化するとき、点 $P$ は、直線 $l$ 上のすべて点を示しています。
これが2点を通る直線のベクトル方程式です。
直線と法線ベクトル
ここまでは直線に平行なベクトルを使って直線のベクトル方程式を考えてきました。
直線に垂直なベクトルを使っても直線のベクトル方程式を作ることができます。
点 $A(\ \overrightarrow{a}\ )$ を通り、$\overrightarrow{0}$ でないベクトル $\overrightarrow{n}$ に垂直になる直線を考えます。
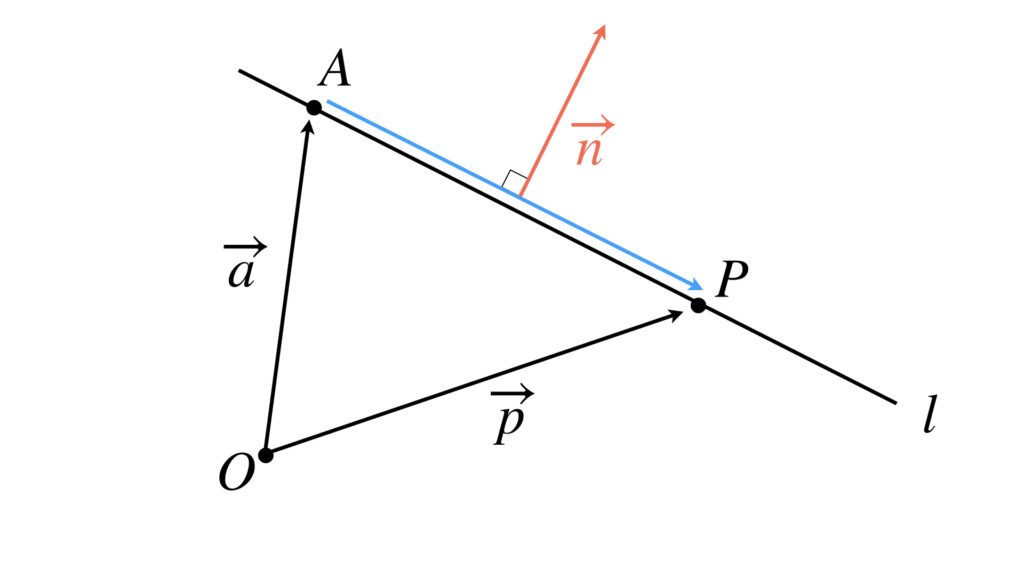
点 $P(\ \overrightarrow{p}\ )$ が直線上にあるのは、次のことが成り立てばいいのです。

この条件を満たすように点 $P(\ \overrightarrow{p}\ )$ を動かせば、その点の集合は直線になります。
$\overrightarrow{AP}\ =\ \overrightarrow{0}$ となっているのは、点$P(\ \overrightarrow{p}\ )$ が点$A(\ \overrightarrow{a}\ )$ と重なってもいいからです。
ベクトル $\overrightarrow{n}$ とベクトル $\overrightarrow{AP}$ が垂直なのは内積を使えば次のように表せます。
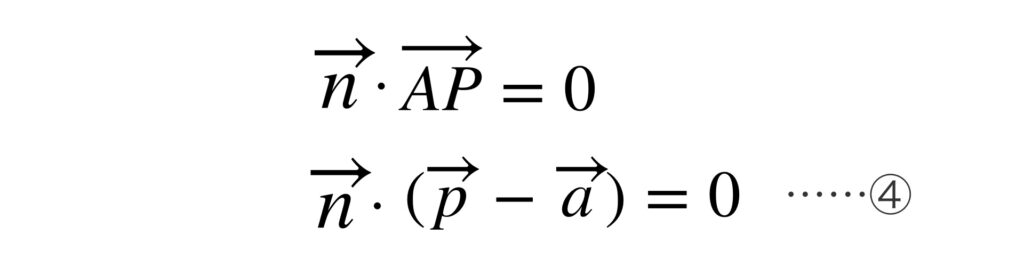
④の式も直線のベクトル方程式です。

直線 $l$ に垂直なベクトル $\overrightarrow{n}$ を直線 $l$ の法線ベクトルといいます。
成分表示による法線ベクトルを使った直線のベクトル方程式
点 $A, B$ の座標とベクトル $\overrightarrow{n}$ の成分を次のようにします。
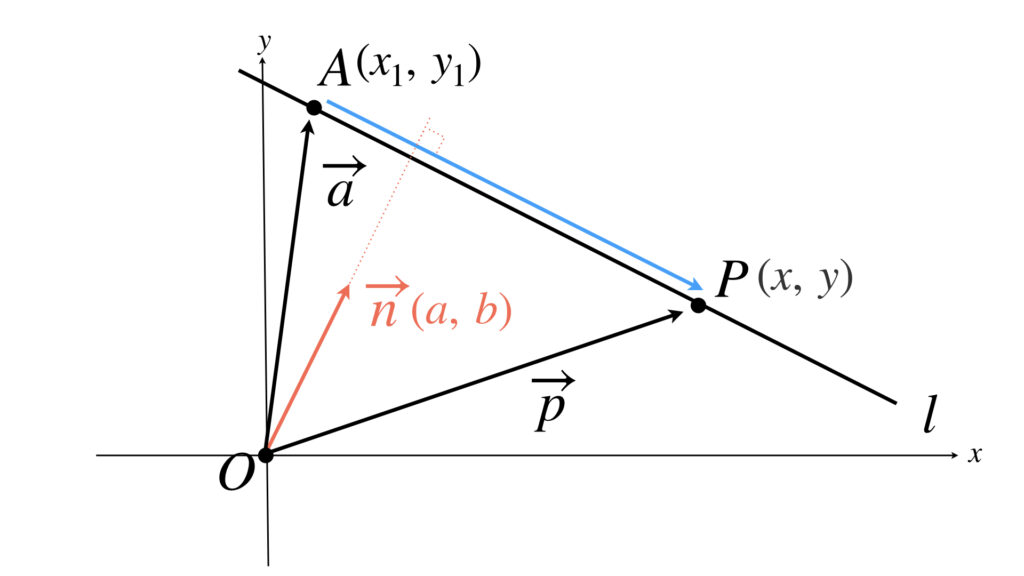
すると④の式は次のようになります。
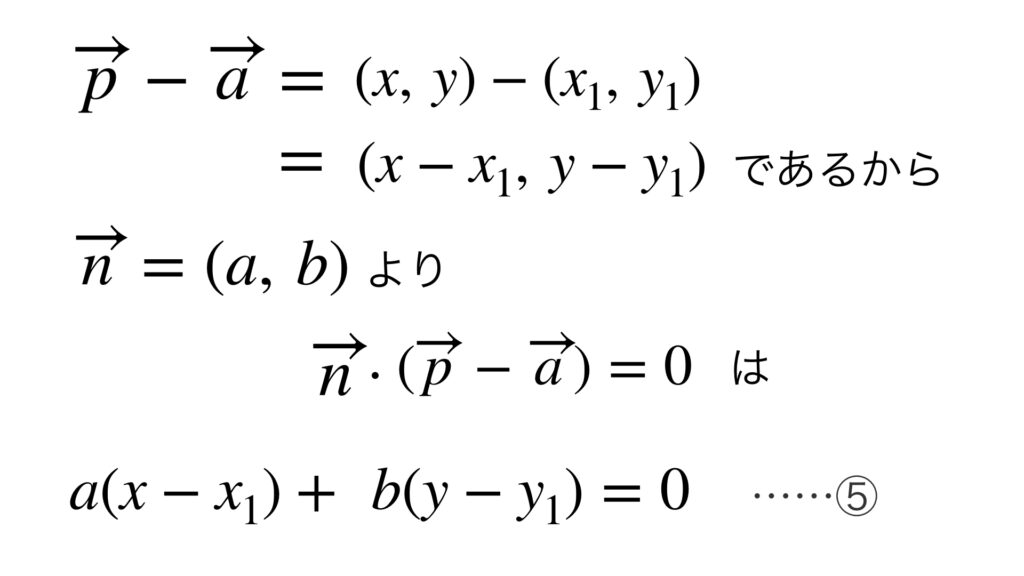
⑤の式を変形させると次のようになります。
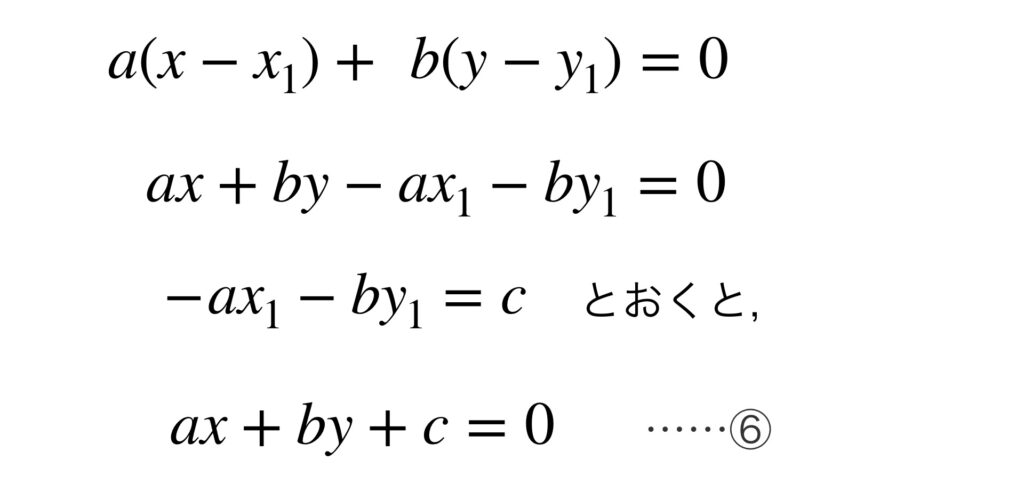
⑥の式は見慣れた直線の方程式です。⑥の式で $\overrightarrow{n}\ =\ (a, b)$ は法線ベクトルの成分になっていることに注意してください。
円のベクトル方程式
点Cを中心とする半径rの円のベクトル方程式
直線ばかりでなく円もベクトル方程式で表せます。
例えば自宅から常に200メートル離れた位置だけを歩けば、人の位置の軌跡は円になります。
この場合、円の中心である家の位置と半径である家からの距離を示せば、人は決まった円上でしか歩けなくなります。
点 $C(\ \overrightarrow{c}\ )$ を中心とする半径 $r$ の円を $K$ とします。
動点 $P(\ \overrightarrow{p}\ )$ が円 $K$ 上にあるためには、ベクトル $\overrightarrow{CP}$ の大きさが常に半径 $r$ と同じになればいいのです。
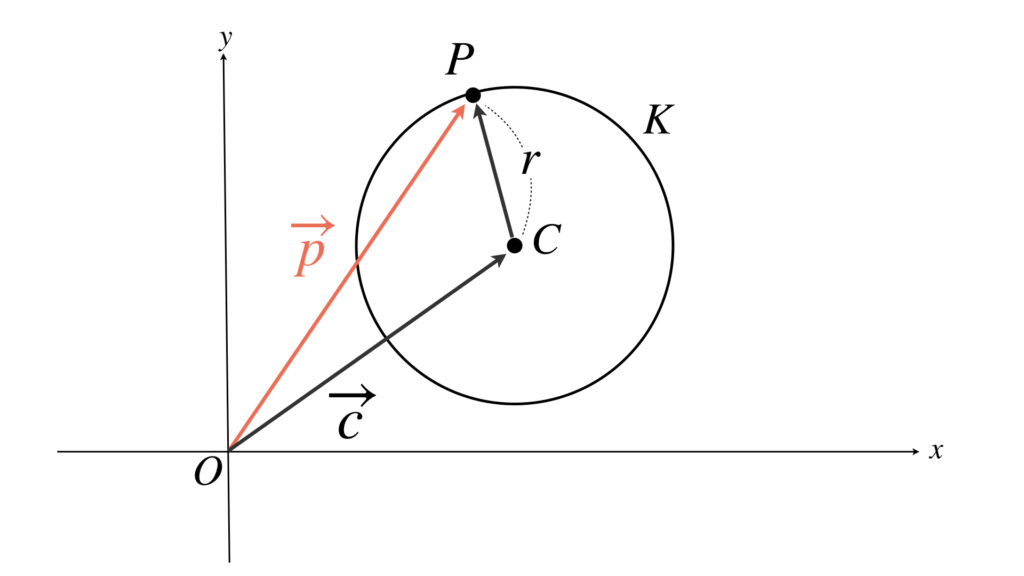
これをベクトルを使って表します。

⑥が円 $K$ のベクトル方程式です。

⑥の式は次のように変形できます。
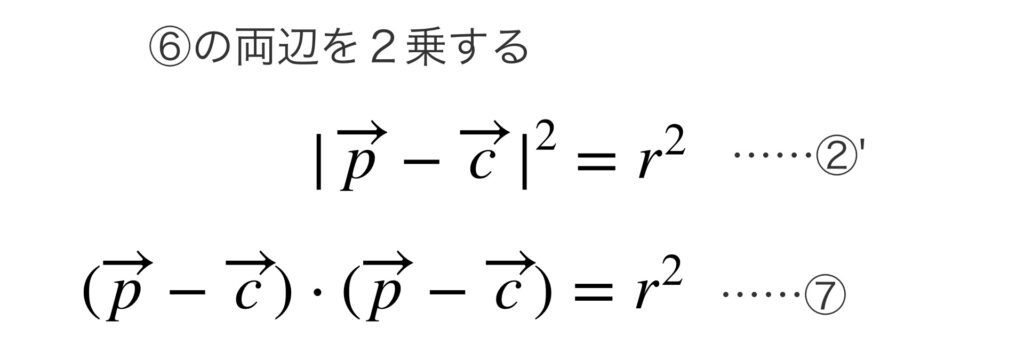
また⑤の式を成分で表せば次のようになります。
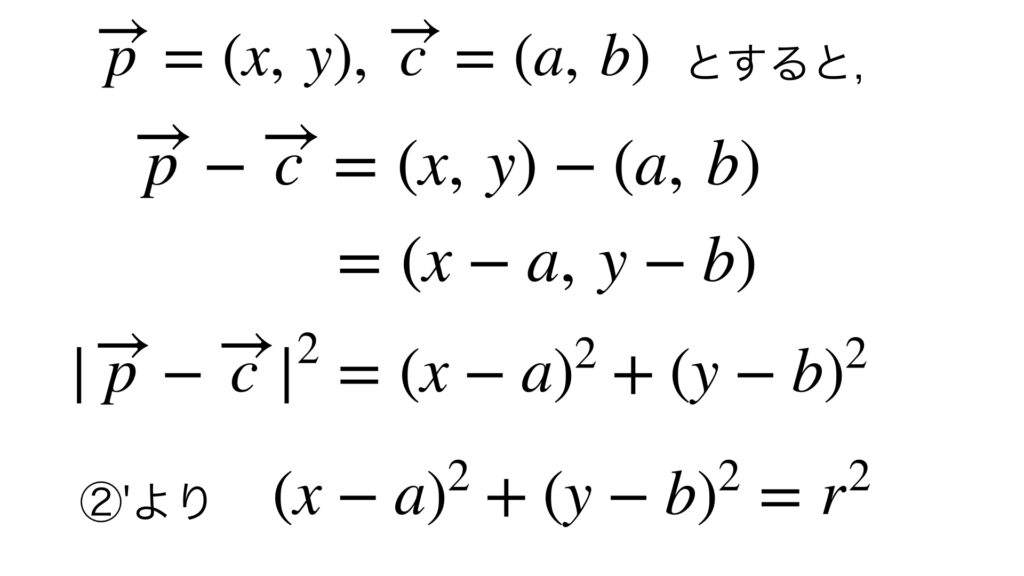
これは見慣れた円の方程式ですね。
線分ABを直径とする円のベクトル方程式
別の条件の与え方を考えます。円についての図形の性質を思い出しましょう。
線分 $AB$ を直径とする円 $K$ で、点 $A, B$ 以外の円 $K$ 上の任意の点を $P$ とすると同一の弧に対する円の中心角と円周角の関係から次のことが成り立ちます。
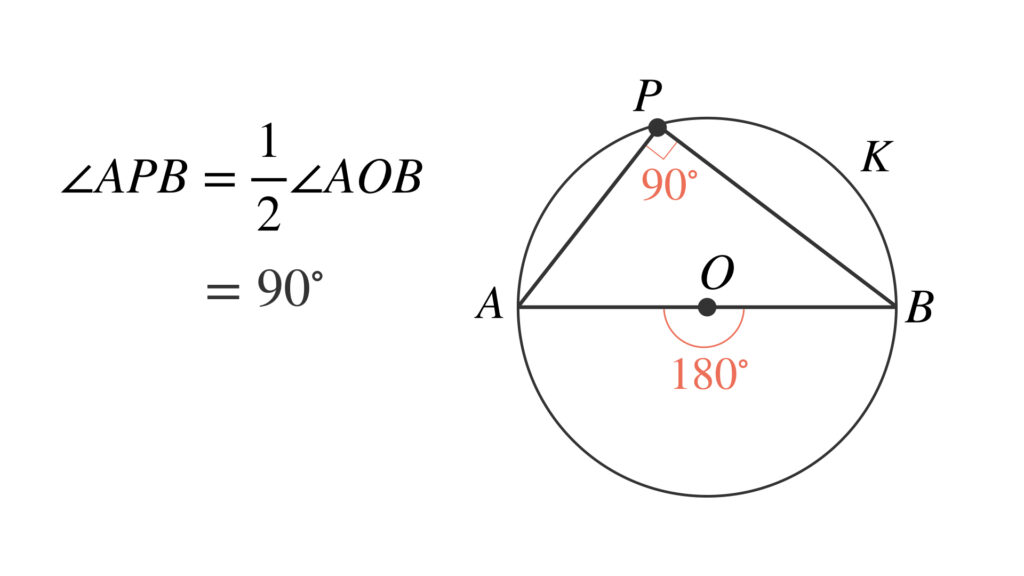
このことを利用します。ベクトルで表します。
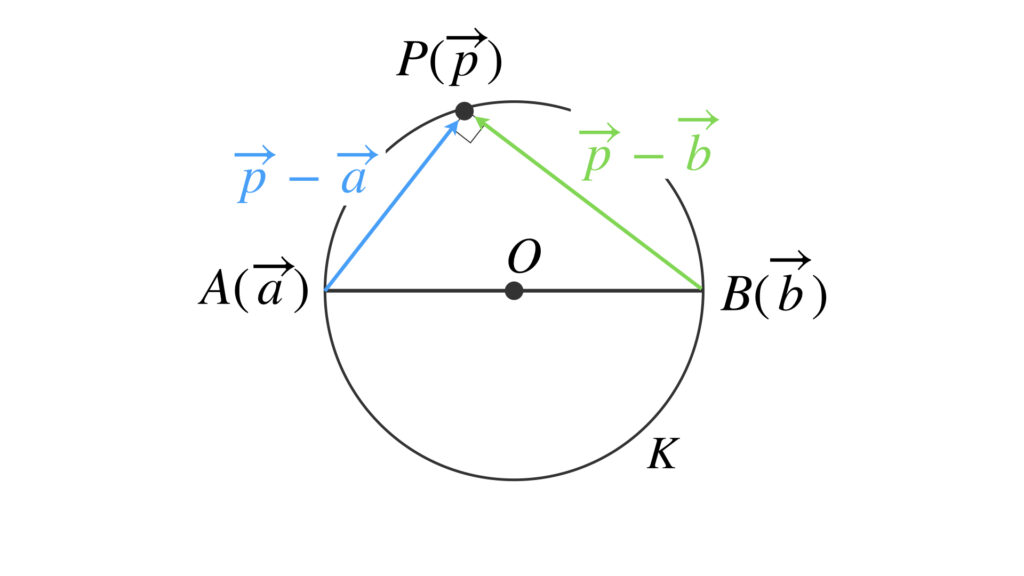
$AP$ と $BP$ が垂直であれば次の式が成り立ちます。
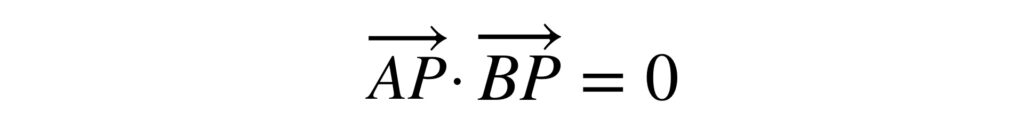
この式は、$P$ が $A$ または $B$ に一致するときにも成り立ちます。
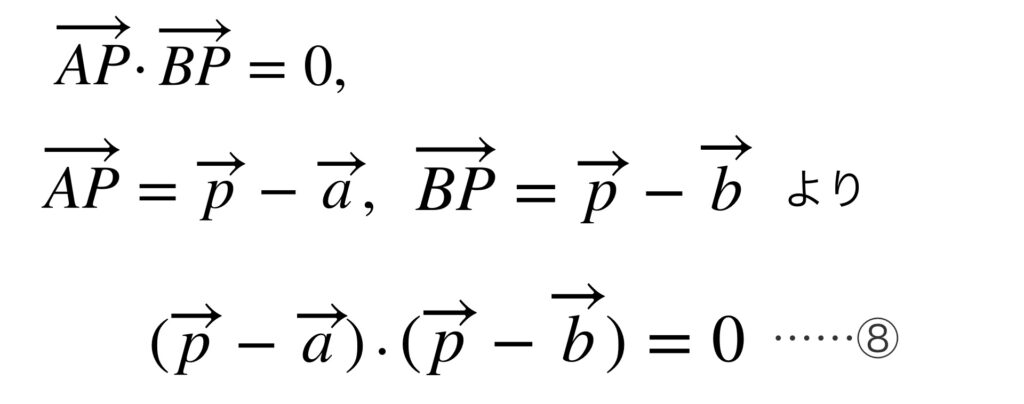
⑧の式も円のベクトル方程式です。

すなわち、この条件に従うように位置ベクトル $\overrightarrow{p}$ で示された点 $P$ は円を描くことになります。
まとめ
位置ベクトルを使って直線や円の方程式を作ることができます。
ベクトル方程式は、式の形が比較的シンプルで方程式の図形的な意味がイメージしやすいのが特徴です。
また空間の位置ベクトルを使って空間図形に拡張する場合にも、基本的な考え方が平面図形と同じなので、とてもスムーズです。
ベクトル方程式の有り難みが本当にわかるのは、空間図形で利用するときかもしれません。
 家庭教師の想い
家庭教師の想い 

