目次
第3問
複数の人がそれぞれ違うプレゼントを1つずつ持ちよって交換会を開きます。全員が自分以外の人の持参したプレゼントを受け取ったところで交換会が終了します。
⑴ 2人または3人で交換会を開く場合
( i ) 2人で交換会を開く場合のすべての配り方を樹形図で表します。$A$ さん、 $B$ さんのプレゼントをそれぞれ $a, b$ とします。
今後、アルファベットの大文字が交換会の参加者で、それぞれの小文字が参加者が持参したプレゼントとします。

これにより2人で交換会を開く場合、1回目の交換で交換会が終了するプレゼントの受け取り方とその確率は次のようになります。


( ii )3人で交換会を開く場合のすべての配り方を樹形図で表します。
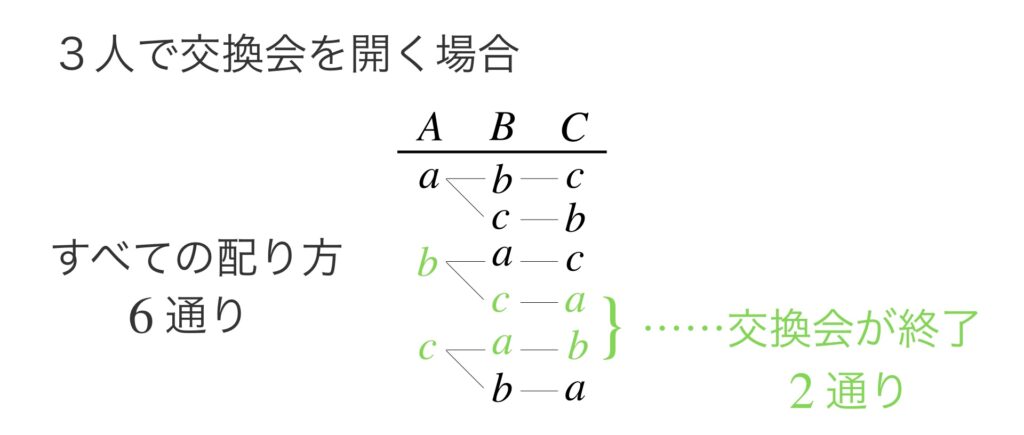
すべての配り方は異なる3文字($a, b, c$)の順列と等しくなります。
これにより3人で交換会を開く場合、1回目の交換で交換会が終了するプレゼントの受け取り方とその確率は次のようになります。

( iii )3人で交換会を開く場合、4回以下の交換で交換会が終了する確率を求めます。
3人で交換会を開く場合、「1回で交換会が終了する確率」はすでに求めてあります。
すると余事象を考えれば「1回で交換会が終了しない確率」も分かりますね。


2回で終了する確率は、「1回目で終了しない確率」に「2回目で終了する確率」を掛ければ求まります(積事象)。
3回で終了する確率は、「1回目で終了しない確率」と「2回目で終了しない確率」と「3回目で終了する確率」を掛ければ求まります。
4回で終了する確率は、「1回目で終了しない確率」と「2回目で終了しない確率」と「3回目で終了しない確率」と「4回目で終了する確率」を掛ければ求まります。
これらをまとめると次のようになります。

そして、これらの事象はすべて排反なので、3人で交換会を開く場合、4回以下の交換で交換会が終了する確率は、これらの確率をすべて足せば求まります(和事象)。

⑵ 4人で交換会を開く場合
1回の交換で、4人のうち、ちょうど1人が自分の持参したプレゼントを受け取る場合を考えます。
たとえば、$A$ さんが自分のプレゼントを受け取り、残りの $B$ さん、$C$ さん、$D$ さんが自分以外のプレゼントを受け取るのは、$B$ さん、$C$ さん、$D$ さんだけで交換会を開き、1回の交換で終了するのと同じなので、つぎのとおり2通りです。

これは $A$ が自分のプレゼントを受け取る場合ですが、自分のプレゼントを受け取る人の決め方はつぎのようになります。

つぎに1回の交換で、4人のうち、ちょうど2人が自分の持参したプレゼントを受け取る場合を考えます。ここでも特定の2人が自分のプレゼントを受け取るときから考えます。
$A$ さんと$B$ さんが自分のプレゼントを受け取り、$C$ さん、$D$ さんが自分以外のプレゼントを受け取るのは、$C$ さん、$D$ さんだけで交換会を開き、1回の交換で終了するのと同じなので、つぎのとおり1通りです。

ですからちょうど2人が自分のプレゼントを受け取る場合は次のようになります。

1回の交換で、4人のうち、ちょうど3人が自分の持参したプレゼントを受け取る場合は、4人全員が自分のプレゼントを受け取るのと同じです。
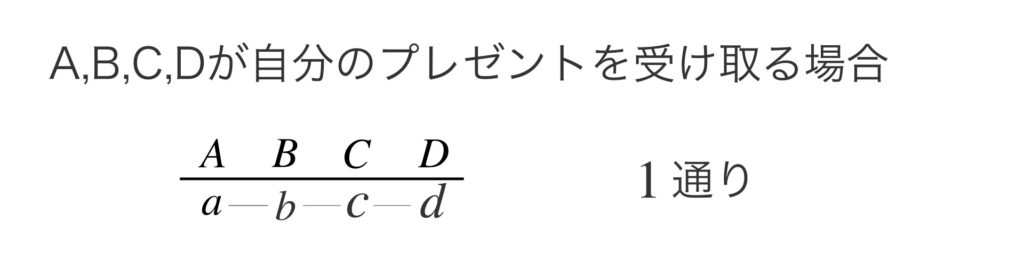
これらをすべて足せば、1回の交換で交換会が終了しない受け取り方の総数が求まります。

1回の交換で交換会が終了する受け取り方は余事象を考えます。

したがって、1回目の交換で交換会が終了する確率は次のように求まります。

⑶ 5人で交換会を開く場合
5人で交換会を開く場合も、4人で交換会を開く場合のときと同様の構想で解いていきます。
1回の交換で、5人のうち、ある特定の1人が自分の持参したプレゼントを受け取り、残りの人たちが自分以外のプレゼントを受け取る場合を考えます。
これは特定の1人を除き、残りの4人だけで交換会を開いて1回目の交換で終了する場合の数と一致します。これは⑵で求めてあり9通りです。
そして自分のプレゼントを受け取る特定の人の選び方を考えれば、5人のうち、ちょうど1人が自分の持参したプレゼントを受け取る場合の数が求まります。

次に1回の交換で5人のうち、ある特定の2人が自分の持参したプレゼントを受け取り、残りの人たちが自分以外のプレゼントを受け取る場合を考えます。
これは特定の2人を除いた残りの3人だけで交換会を開き1回の交換で終了する場合の数に一致します。
これもすでに求めてあり2通りです。そして自分のプレゼントを受け取る特定の2人の選び方を考えれば、5人のうち、ちょうど2人が自分の持参したプレゼントを受け取る場合の数が求まります。

次に1回の交換で5人のうち、ある特定の3人が自分の持参したプレゼントを受け取り、残りの2人が自分以外のプレゼントを受け取る場合を考えます。これは1通りです。そして自分のプレゼントを受け取る特定の3人の選び方を考えれば、5人のうち、ちょうど3人が自分の持参したプレゼントを受け取る場合の数が求まります。

1回の交換で5人のうち、ある特定の4人が自分の持参したプレゼントを受け取るのは、もはや全員が自分のプレゼントを受け取るのと同じですから1通りです。

これらを足せば5人で交換会を開く場合に1回の交換で終了しない場合の数が求まります。

そして余事象を考えます。

したがって、1回目の交換で交換会が終了する確率は次のように求まります。

⑶ 条件付き確率
条件付き確率の定義を確認しましょう。

今回の問題では事象 $A$ と事象 $B$ は次のようになります。

事象 $A$ には $E$ については書かれていません。つまり $E$ は自分のプレゼントを受け取っても受け取らなくても、どちらでも構わないということです。
$E$ についても記述に含めて事象 $A$ を表せば次のようになります。

では「または」で連結されたそれぞれの事象の場合の数を考えましょう。
「1回目の交換で $A, B, C, D, E$ がそれぞれ自分以外の人のプレゼントを受け取る場合」とは「5人で交換会を開き、1回目の交換で交換会が終了する」場合と同じですから⑶で求めたとおり「44通り」です。
また「1回目の交換で $A, B, C, D$ がそれぞれ自分以外のひとの持参したプレゼントを受け取り、$E$ が自分のプレゼントを受け取る」のは 、$E$ 以外の $A, B, C, D$ 4人だけで交換会を開き、1回目の交換で交換が終了する場合の数と同じですから ⑵ で求めたとおり「9通り」です。
そして、この2つの事象は互いに排反なので、事象 $A$ の場合の数は足して「53通り」となります。
では $A$ かつ $B$ の場合の数はどうなるでしょうか。これは「5人で交換会を開き、1回目の交換で終了する」のと同じ事象ですね。

ですから、この場合の数は「44通り」となります。
ではこれまでに求めた場合の数を使って条件付き確率を計算しましょう。

まとめ
この問題も出題者の意向(構想)に沿って解いていけば解答が得られるようになっています。
効率よく解くためには、すでに出した答えを次の問題を説くときに利用できなければなりません。共通テストの問題は、ひとつひとつが有機的なつながりを持っているのです。
苦手になりやすい条件付き確率は、問題を解きやすくするために少し問題文を読み替える必要があります。それができるようになれば条件付き確率を得意にできます。
 家庭教師の想い
家庭教師の想い 

