指数までなら何とかなったのに、対数に入ったら全くお手上げ状態になる人っていますね。そのような人のために対数を説明します。
目次
先ずは指数関数を確認しましょう
先ずは関数から説明します。
なぜ関数の話から始めるのかと言うと、あなたが指数までなら何とかなって対数に入ったらつまずいたという事実から「これは関数から教えるべきだな」と経験上分かるからです。これを知らずに進んだら、いつまで経っても指数・対数に対してモヤモヤした感じが拭いきれないでしょう。
関数ってこんなもの
では関数を直感的に理解するところから始めましょう。次のような箱を想像してみてください。その箱には左右ふたつ穴が開いていて、そのひとつの穴から数を入れると反対側の穴から数が出てきます。
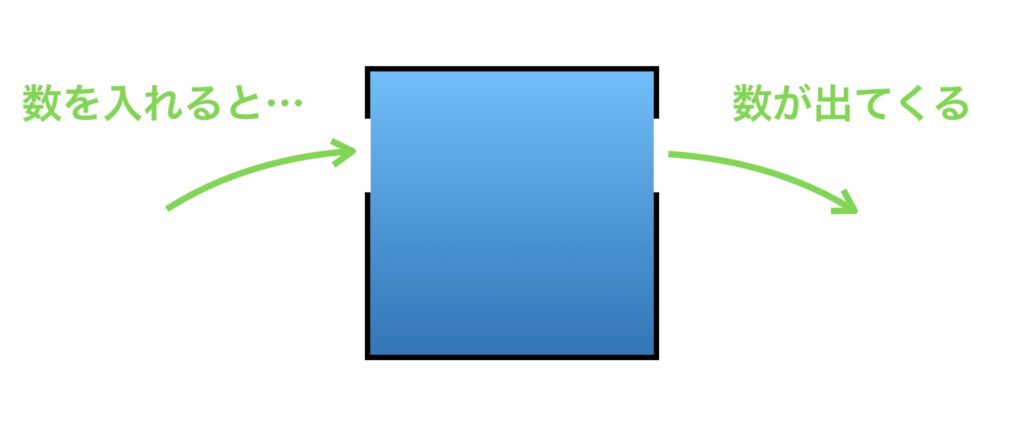
では実際に数を入れてみましょう。1を入れてみます。
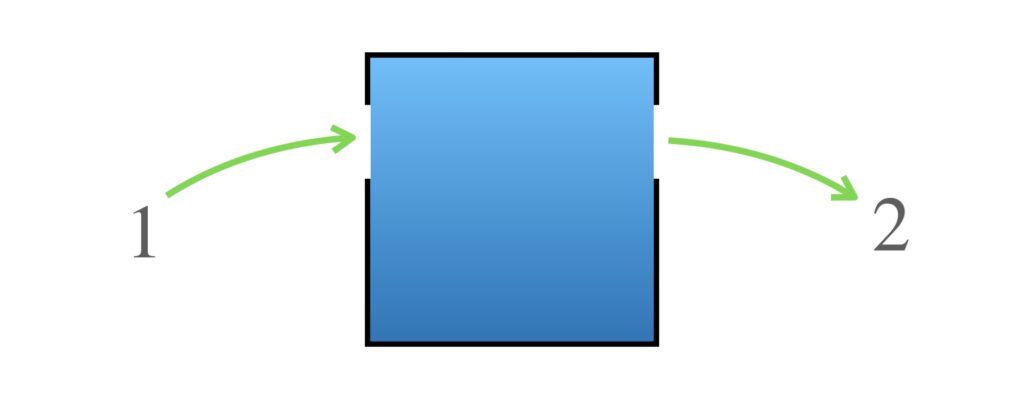
2が出てきました。では次に2を入れてみましょう。
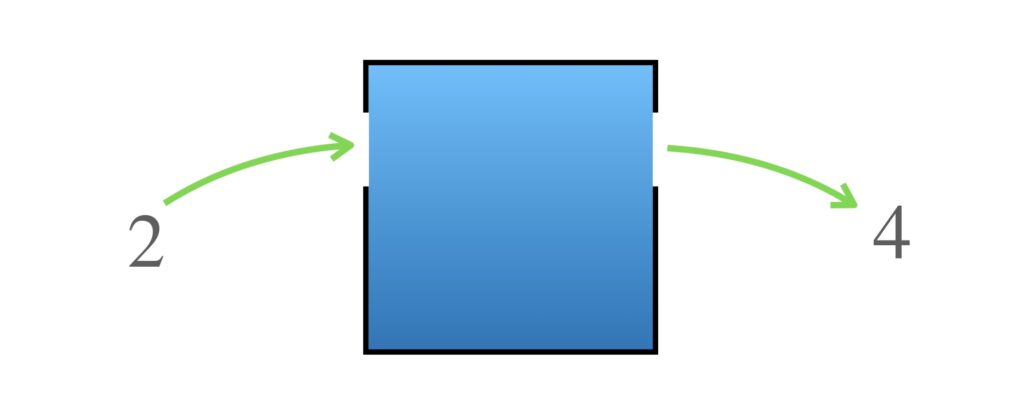
4が出てきました。3を入れると…
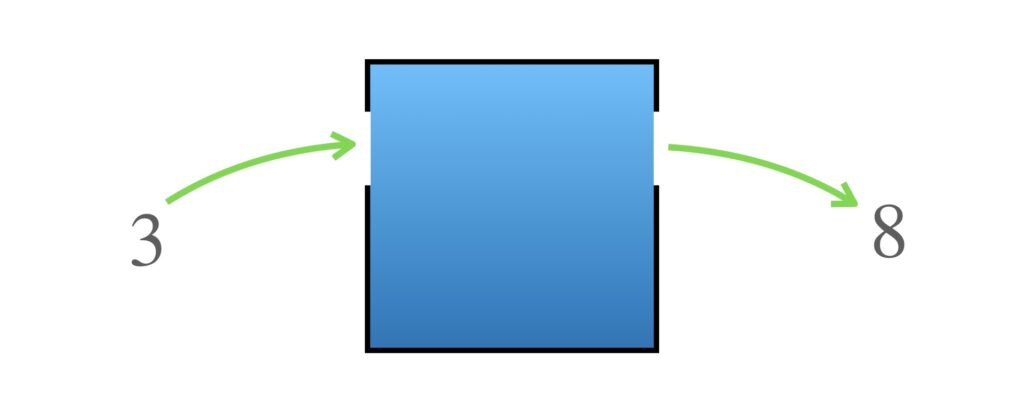
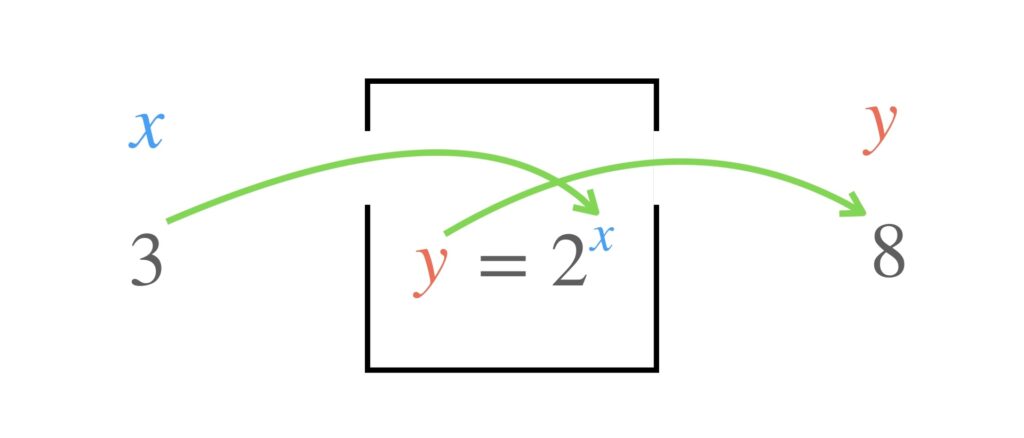
もう分かりましたね。箱の中を覗くと次のような関数の式が入っていました。指数関数ですね。入れる数を x とすれば出てくる数は y です。
指数関数のグラフ
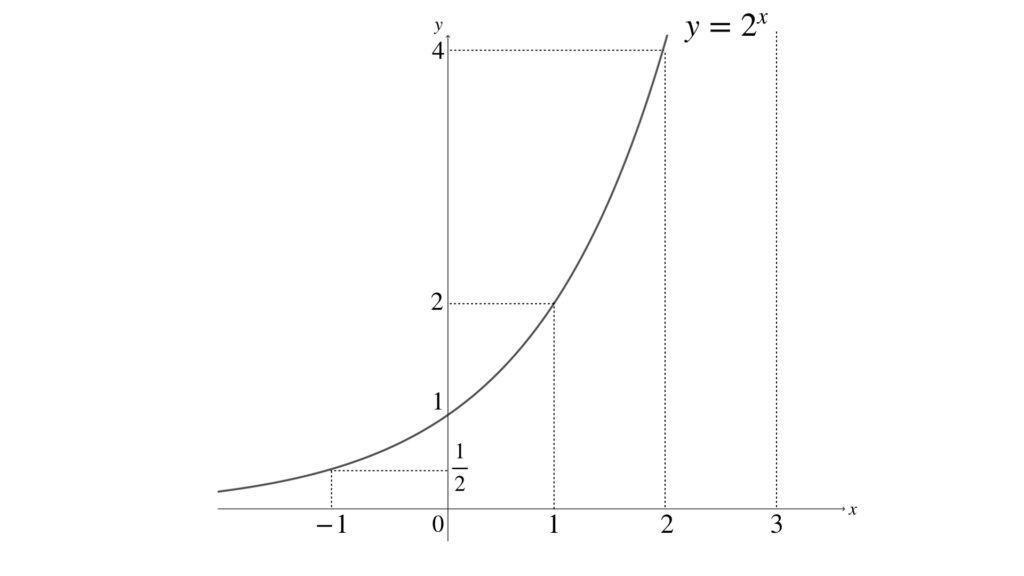
全ての実数を x に入れて、この関数の x – y グラフを作ると次のようになります。
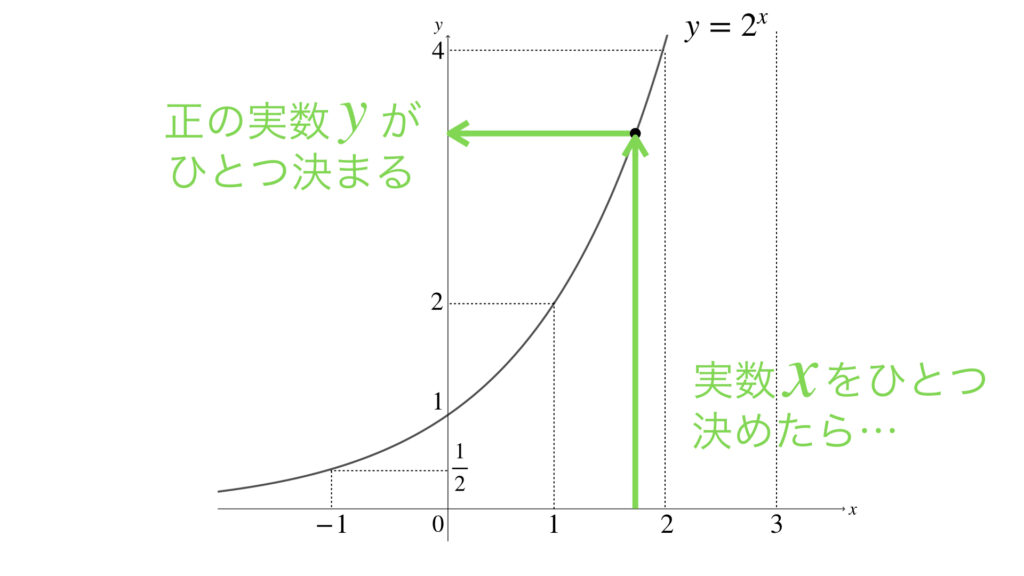
このグラフを見て分かるとおり、実数ならどんな数を x に入れても、それに対応した実数 y がただひとつ決まることがわかります。また、出てくる y は正の実数であることも確認しておきましょう。
ではもう一度試してみます。x に π (パイ) を入れてみます。π だって実数ですから大丈夫のはずですが出てきたのは…
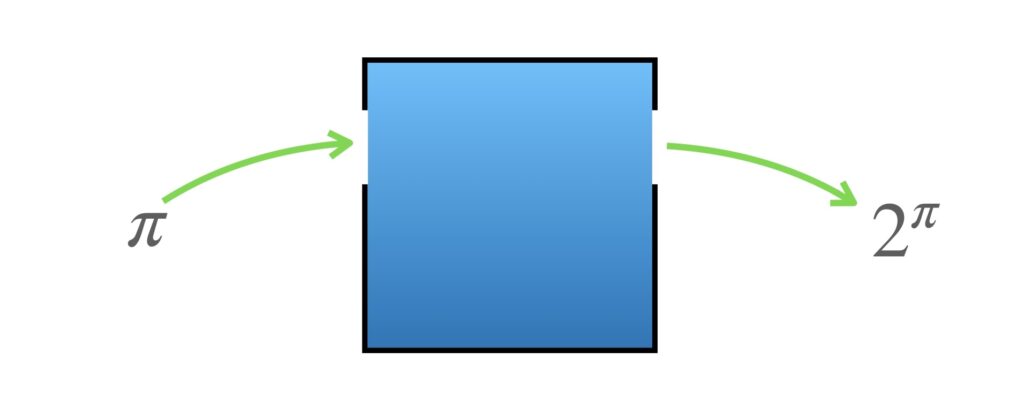
なんだか手抜きをされたように思えますが、でも出された値は正しいものです。つまり小数のような値を出してくれなくても、出したい値の表現方法はあるので、ともかく、この箱は、どんな実数を入れられても、それに対応する正しい値を吐き出してくれます。
では今度は反対側の穴から、つまり y に数を入れてみましょう。先程 y は正の数しか出てこないと知ったので、 y には正の実数しか入れてはダメですよ。
2を入れると…
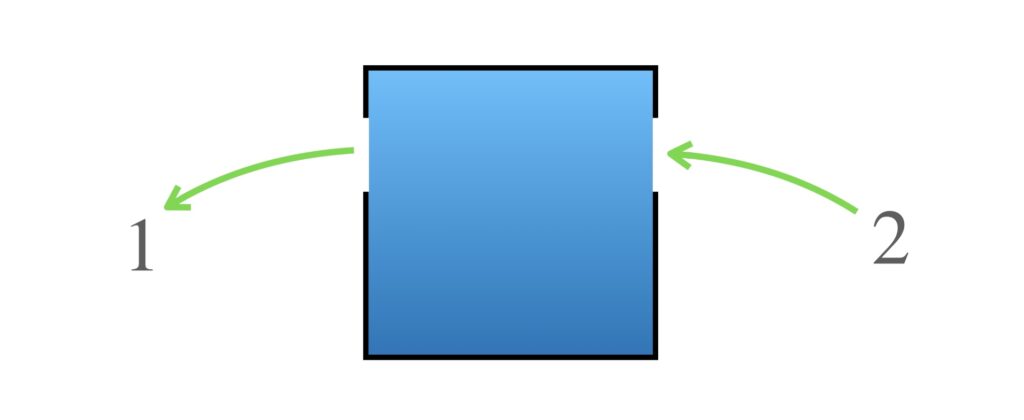
4を入れると…
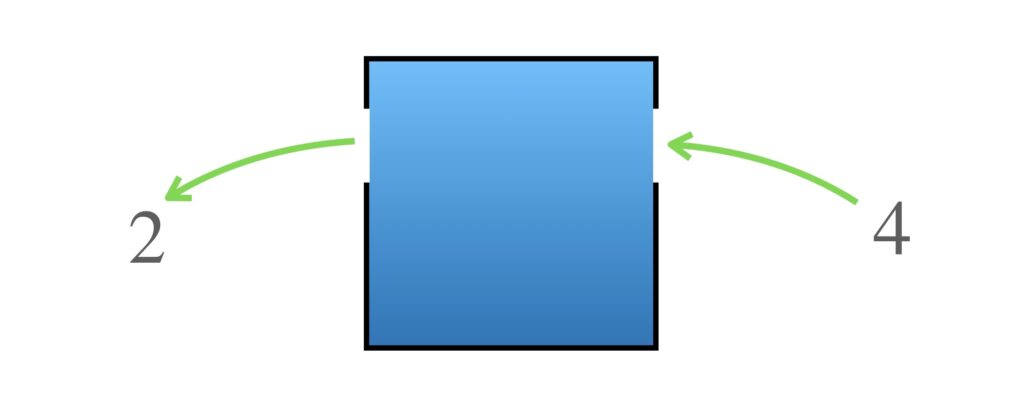
8を入れると…
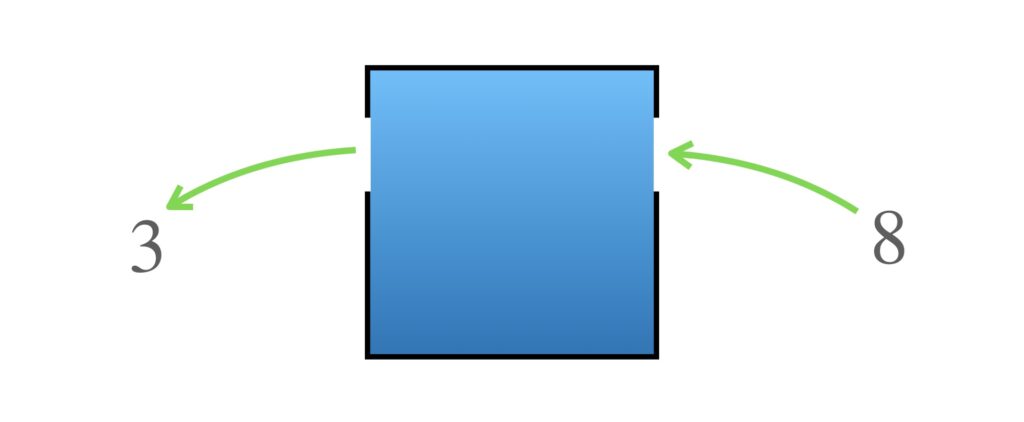
ここまでの結果は予想通りです。でも y は正の実数なら全て大丈夫なはずですよね。それはグラフから明らかです。
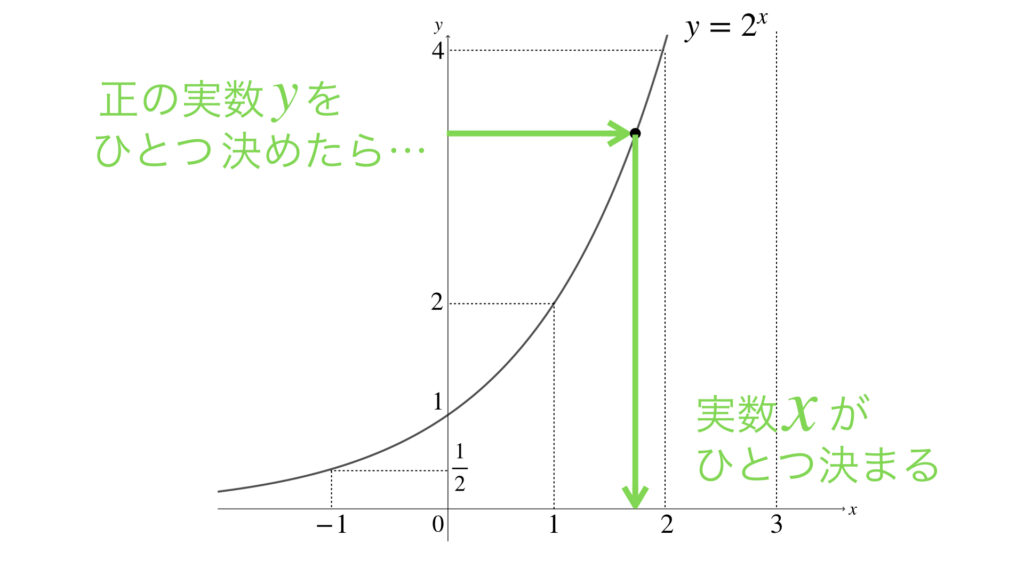
だったら y に3を入れてみましょう。どうなるでしょうか?出てくる値を想像してみてください。
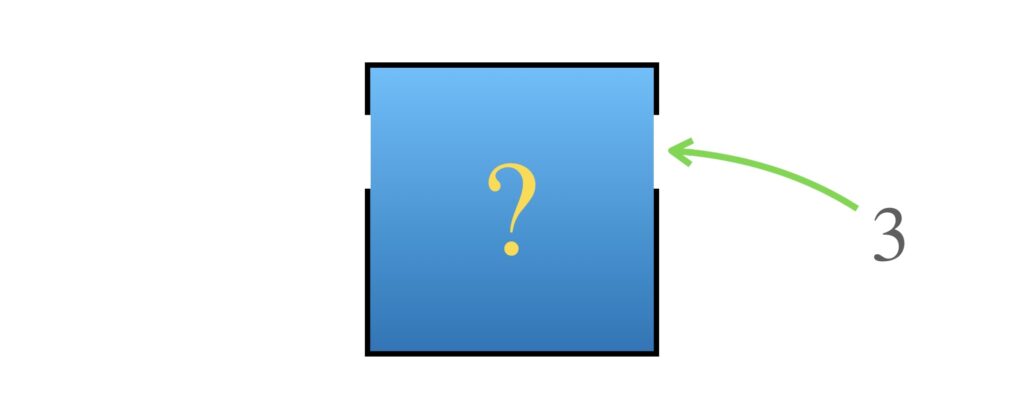
あれ?値を出してくれませんね。なぜでしょうか?実は、さっき箱の中にある関数だけでは、反対側から数を入れられると、計算はもとより表現方法さえないので値を出すことができないのです。それでは困りますね。だって y に対応する x が必ずあることはグラフからも明らかだからです。ではちゃんと x が出てくるようにこの箱を改良しましょう。
対数(log)の定義
そこで登場するのが対数です。対数は次のように定義されています。

ところで底は1ではない正の実数です。真数は正の値でなければなりません。
定義を読んだだけでは分かりにくいですね。ではこの定義の意味を具体的な数値を使って確認しましょう。
例えば4という数値があって、これは2の何乗なのか考えます。
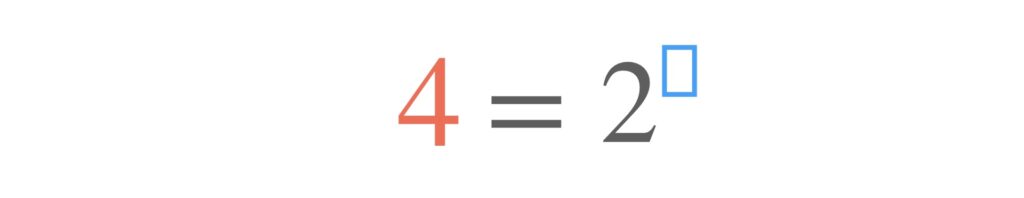
この四角の中に入る値が対数です。これなら四角の中は2だとすぐわかりますね。
でも3は2の何乗なのかを考えると…

いくら考えてもわかりません。でも対数の定義に従って四角に入れる数値を表せば次のようになります。

この定義があれば、すべての正の実数の対数を表せるのです。では対数を使って箱の機能を完成させましょう。次のような関数を用意します。
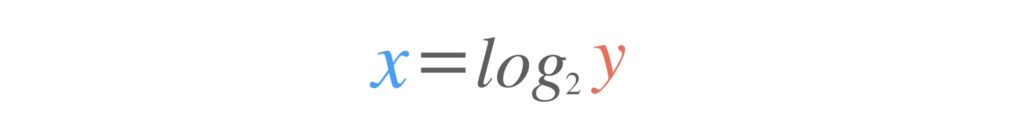
これをさっきの箱の中に加えます。
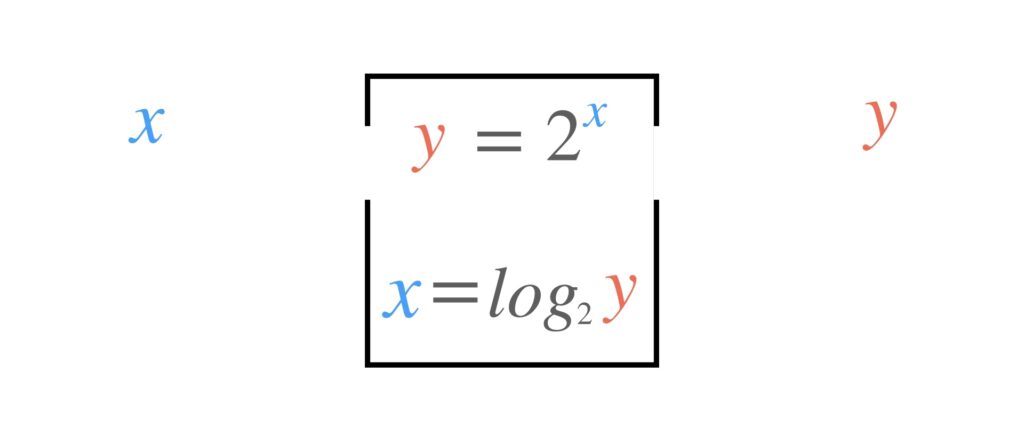
これで準備ができました。では、もう1度 y に3を入れてみましょう。
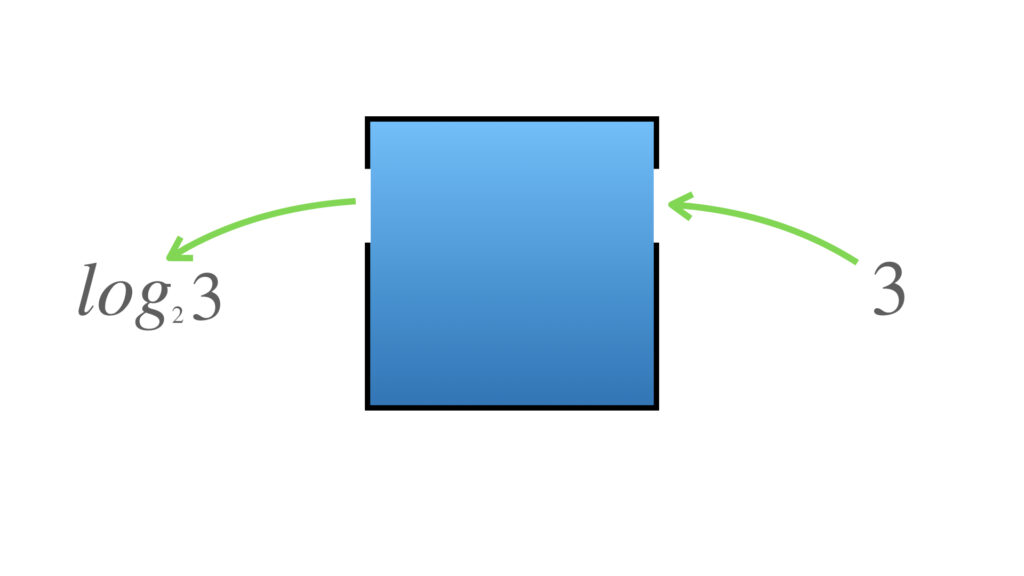
定義通りに解釈すれば、出てきた x は、小数にしてくれなくても正しい値です。これで、この箱の機能は完全になりました。
まとめ
もう一度この箱の中にある関数の式を見てみましょう。
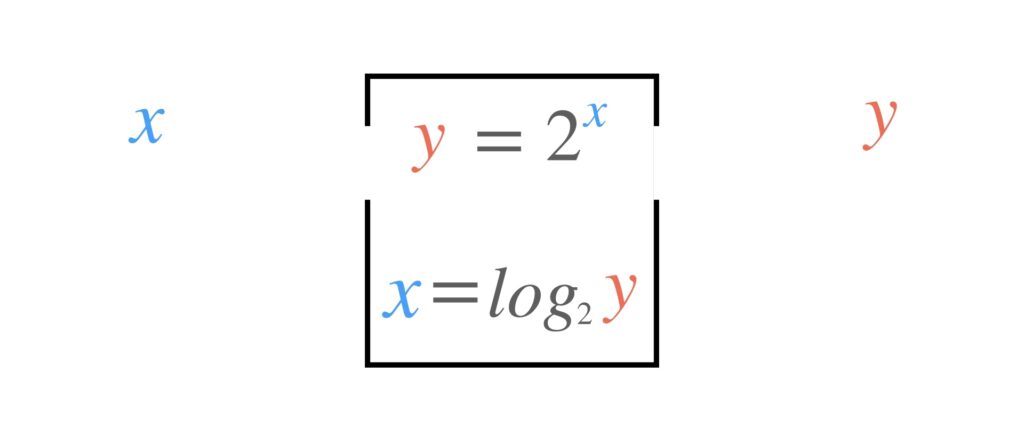
元々入っていた指数関数と加えた対数関数は、x と y の関係を表している点では同じです。ただ入れる数と出てくる数が逆になっています。

このようなふたつの関数は、互いに「逆関数」の関係にあると言えます。
「2の3乗はいくつですか?」の質問に答えるための式が
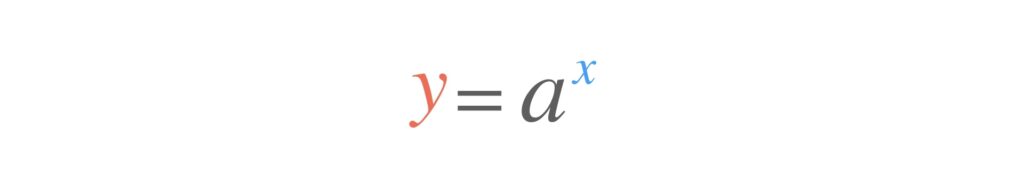
です。a に2、x に3を代入すれば、この質問の答えである y が8と求まります。
そして「8は2の何乗ですか?」に答えるための式が
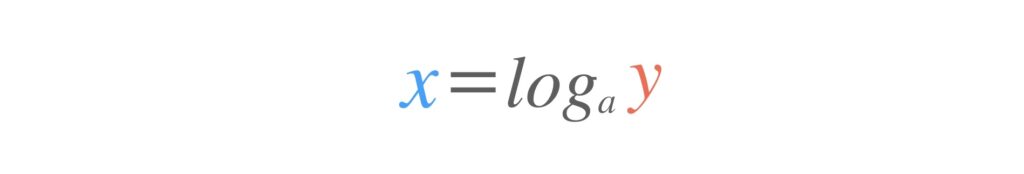
です。答えはもちろん3ですね。a に2、y に8を代入すれば、この質問の答えである x が3と求まります。
もし「3は2の何乗ですか?」と聞かれたら、

と答えればいいのです。
 家庭教師の想い
家庭教師の想い 

