平方根の値として覚えているのは$\sqrt{2}$ 、$\sqrt{3}$、$\sqrt{5}$ ぐらいでしょうか。
平方根を含んだ問題を解いていて、いっそのこと「平方根の近似値がわかってしまえばいいのに」と思ったことはありませんか?
じつは平方根の近似値は筆算で求められます。
今回は、そのやり方を、これ以上ないほどのわかりやすさで説明します。
目次
平方根を筆算で求める
では、実際に次の数の平方根をもとめてみましょう。

まず小数点の位置から2桁ずつ区切ります。そして割り算の筆算を行うときと同様に、下のように書きます。

つぎに、いちばん高い桁の位置にある $6$ に着目します。
$6$ 以下で $6$ にもっとも近い平方数をみつけます。
それは $2^2=4$ ですね。 この平方数を与える $2$ を $6$ の上に立てます。

$2$ の平方数である $4$ を $6$ の下に書いて $6$ から引きます。
立てた $2$ は、次のように別な場所にも書き $2+2=4$ を計算しておきます。
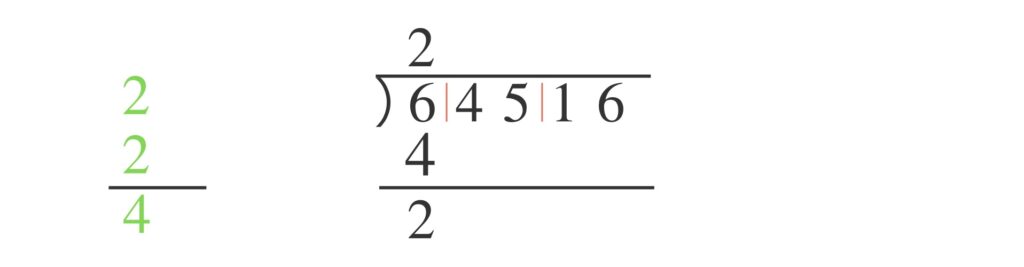
$45$ を下ろします。
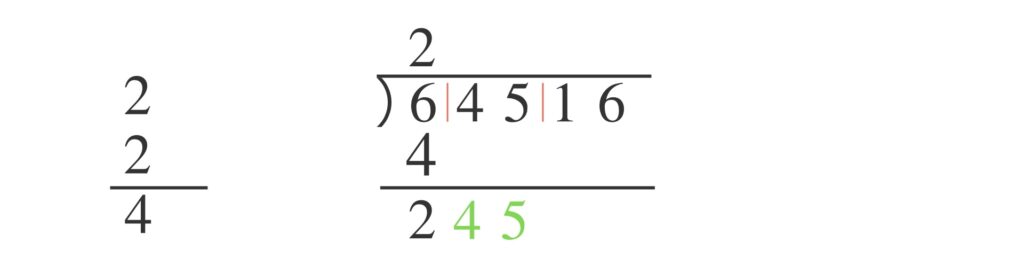
つぎに $2+2$ の答えの $4$ の横に、四角を縦にふたつ並べて書きます。
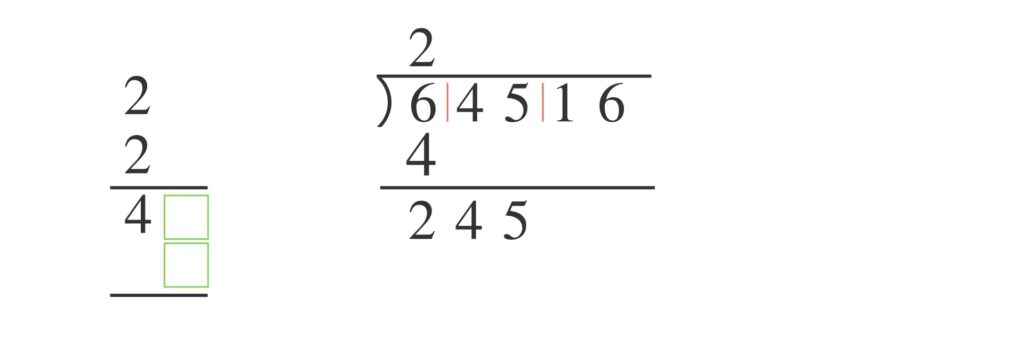
この四角の中に同じ整数を入れ、縦に並んだ2つの数をかけて $245$ 以下で $245$ にもっとも近い数を求めます。それは $ 45 \times 5=225$ ですね。
四角の中に入れた数を、すでに立ててある $2$ の右横に立てます。そして $ 45 \times 5$ で求めた数を $245$ の下に書き引き算します。 $20$ となります。
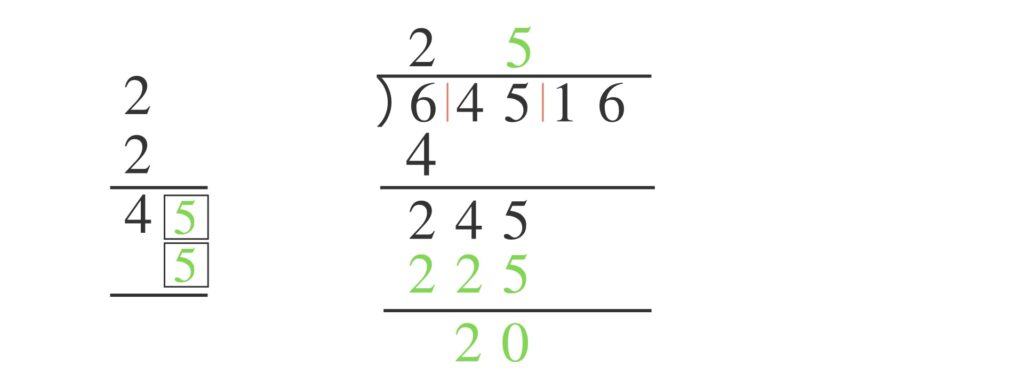
次に $16$ を下ろします。 $45$ と$5$ は足し算ておきます。
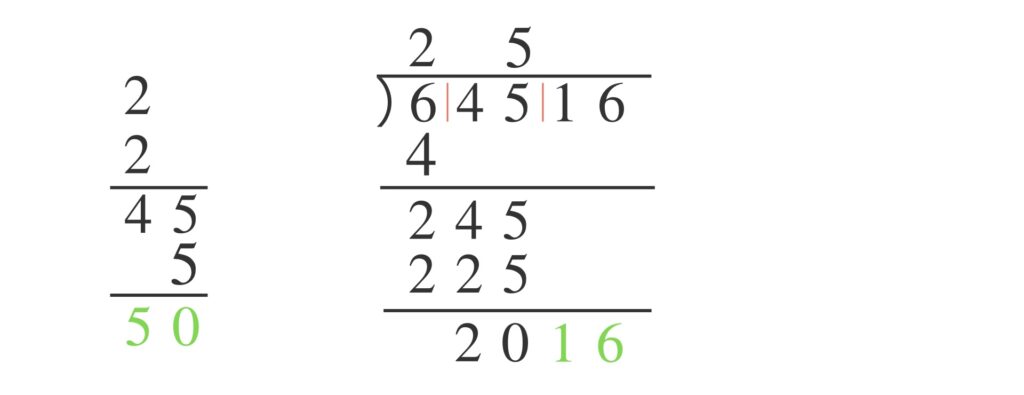
足し算の答えの $50$ の横に四角を縦にふたつ並べて描きます。
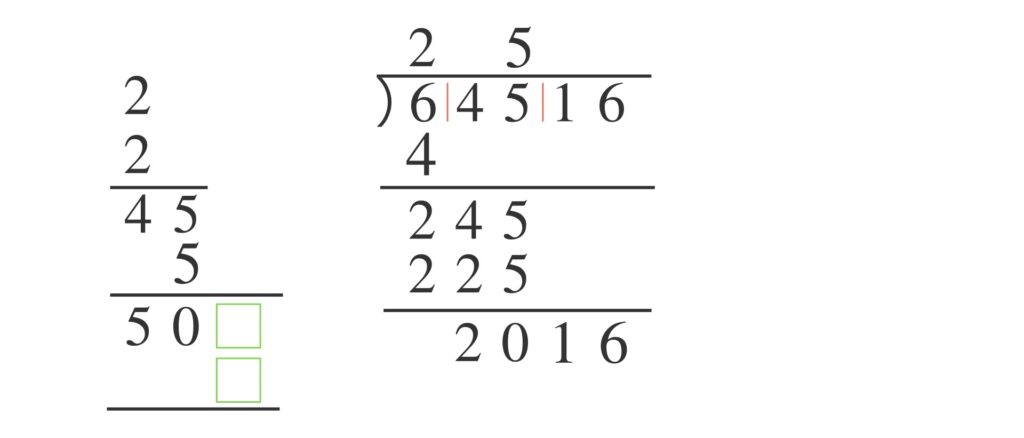
この四角の中に同じ整数を入れ、縦に並んだ2つの数をかけて $2016$ になる数を求めます。

四角に入れた数 $4$ を $5$ の右横に立てます。そして求めた数を $2016$ の下に書き、引き算します。これが $0$ になれば計算終了です。
いちばん上に立っている $245$ が $64516$ の正の平方根です。
近似値をもとめてみよう
先程の手順を繰り返せば平方根の近似値が求められます。
次の近似値をもとめてみましょう。
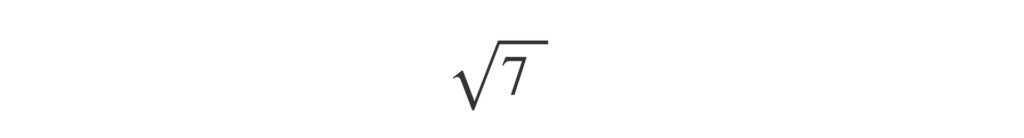
やはり小数点の位置から2桁ずつ区切り、下のように書きます。
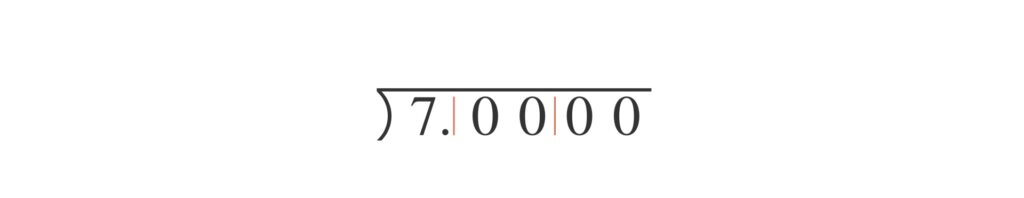
$7$ 以下で $7$ にもっとも近い平方数をみつけます。その平方数を与える $2$ を $7$ の上に立てます。

$2$ の平方数である $4$ を $7$ の下に書いて $7$ から引きます。
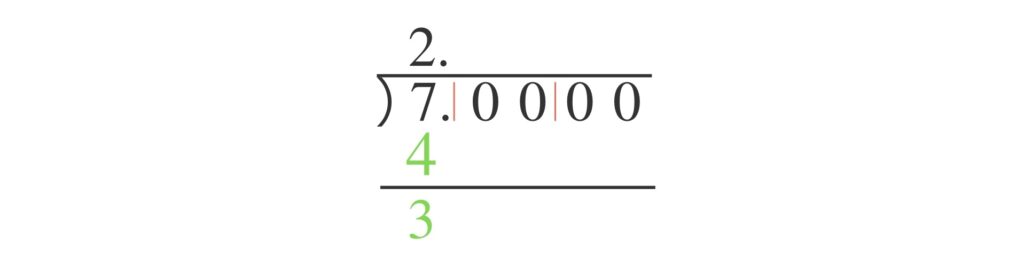
立てた「$2$」を次のように別な場所に書き $2+2=4$ を計算しておきます。
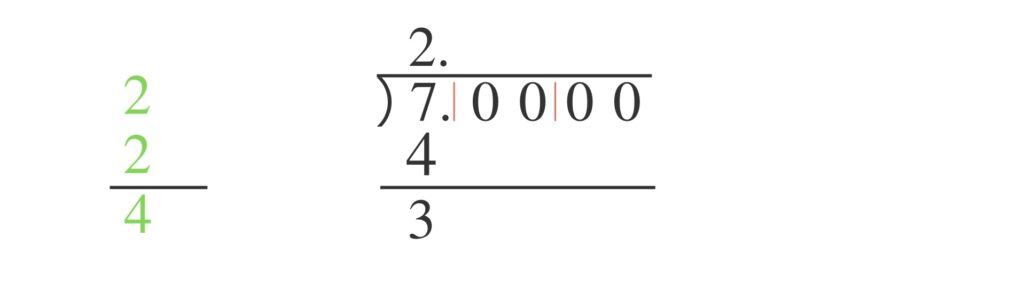
$00$ を下ろします。
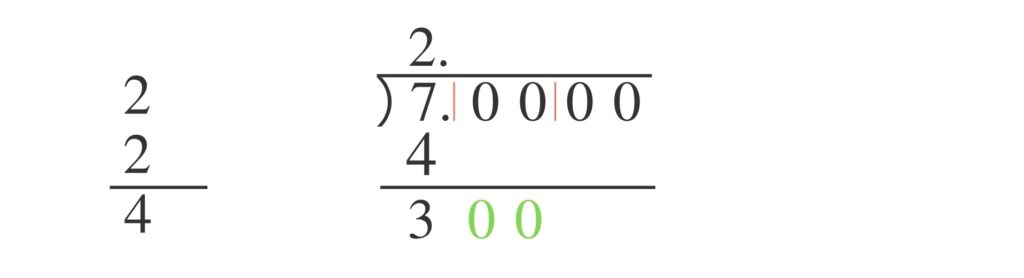
つぎに $2+2$ の答えの $4$ の横に、四角を縦にふたつ並べて描きます。
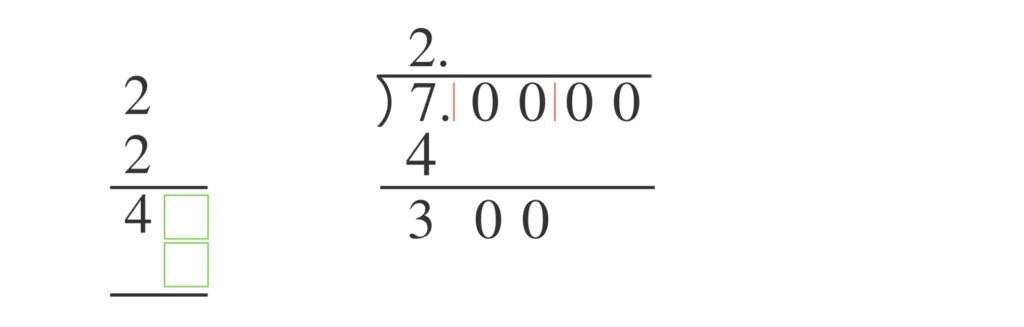
この四角の中に同じ整数を入れ、縦に並んだ2つの数をかけて「$300$」以下で「$300$」にもっとも近くなる数を求めます。
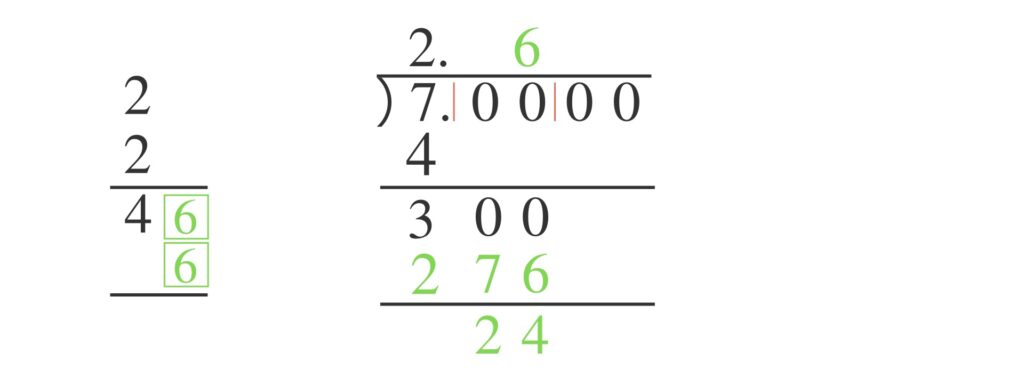
四角の中に入れた数を、すでに立ててある $2$ の右横に立てます。そして求めた数を「$300$」の下に書き、引き算します。
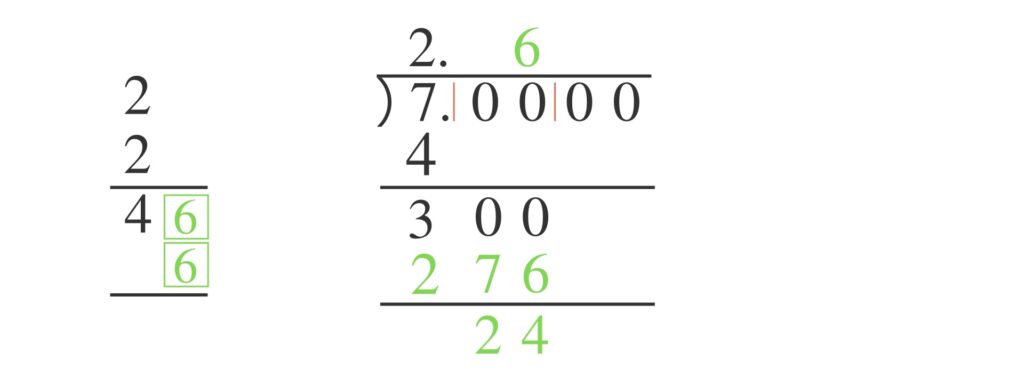
次の「$00$」を下ろします。 $46$ と$6$ は足し算しておきます。
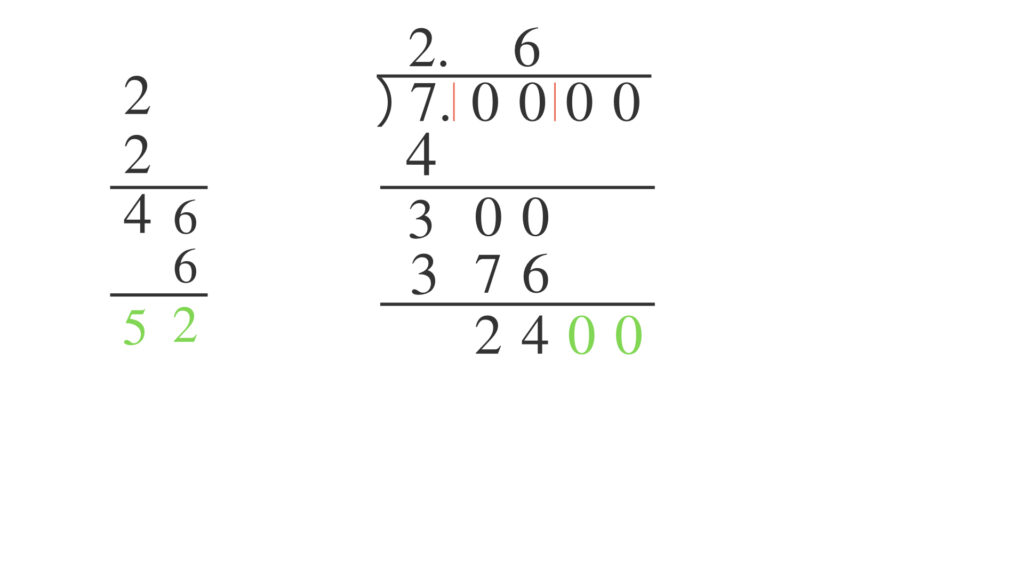
つぎに足し算の答えの $52$ の横に四角を縦にふたつ並べて描きます。

この四角の中に同じ整数を入れ、縦に並んだ2つの数をかけて $2400$ 以下で $2400$ もっとも近い数をみつけます。
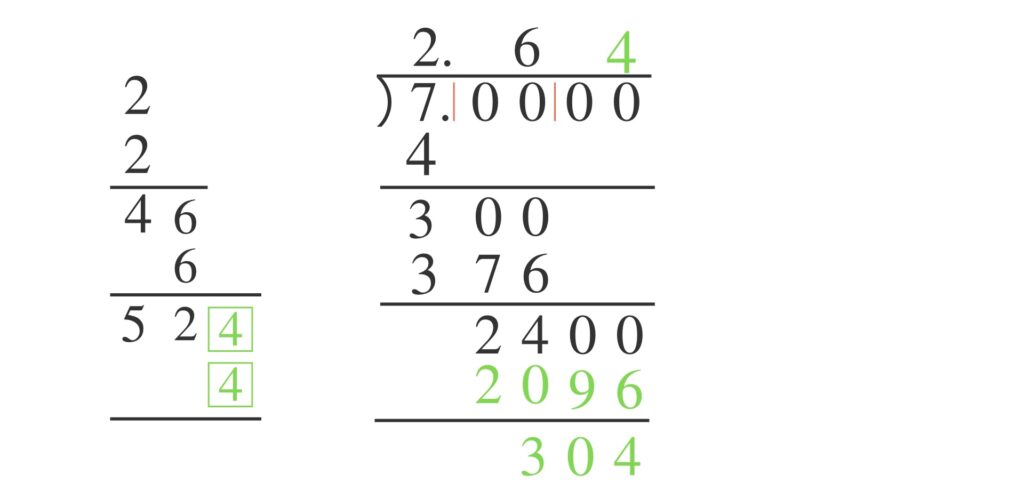
四角の中に入れた数を、すでに立ててある $6$ の右横に立てます。そして求めた数を $2400$ の下に書き、引き算します。
この操作を繰り返せば近似値を永遠に求めることができます。この時点では、いちばん上に立っている $2.64$ が $\sqrt{7}$ の小数第2位までの近似値です。
開平の仕組み
では、なぜこのような操作で平方根を求められるのでしょうか?正方形の面積を使って考えてみましょう。
面積がわかっている正方形
百の桁が $a$ 、10の桁が $b$ 、1の桁が $c$ である自然数を考えます。これを1辺とする正方形を考え、その面積を $S$ とします。
この面積 $S$ が概知で $a$、$b$、$c$ を求めるのが平方根 $\sqrt{S}$ の計算です。
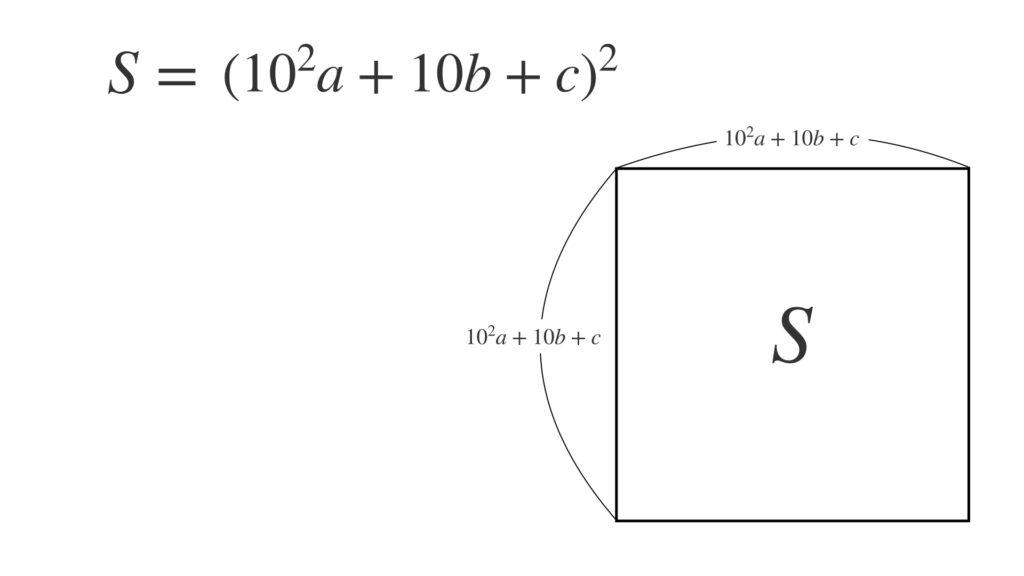
式を展開して次のように整理します。
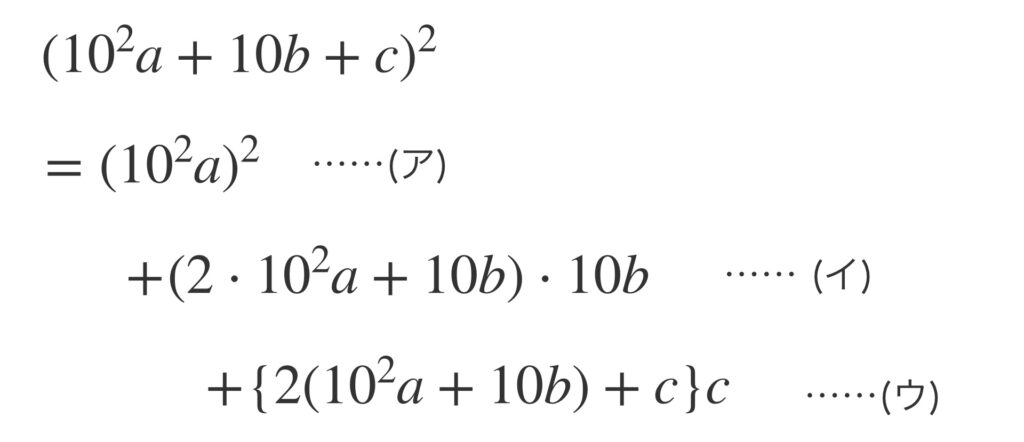
この式の(ア)と(イ)と(ウ)について、それぞれの意味を考えましょう。
最初は(ア)です。
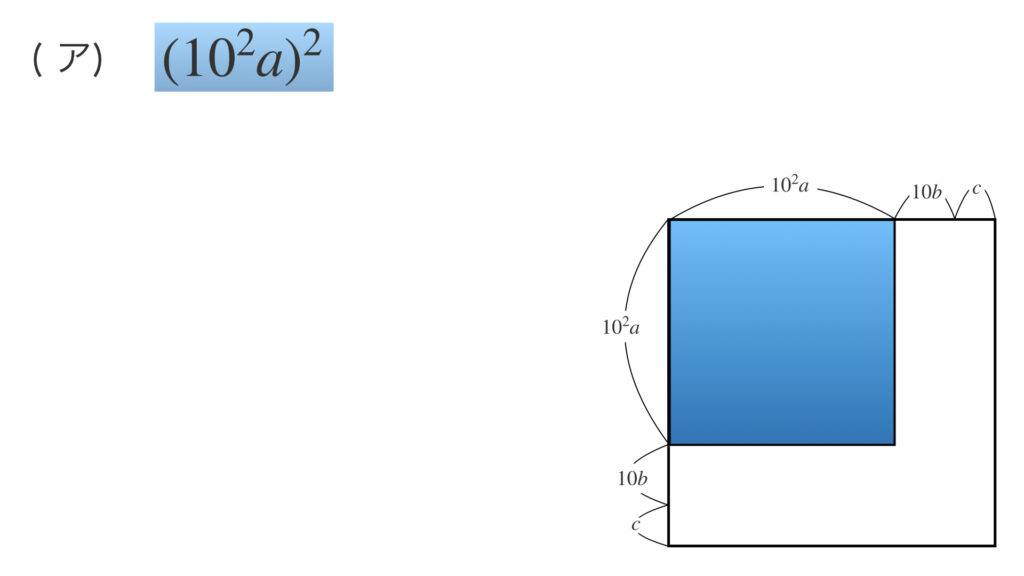
これは図の青色の面積を意味しています。
次は(イ)です。
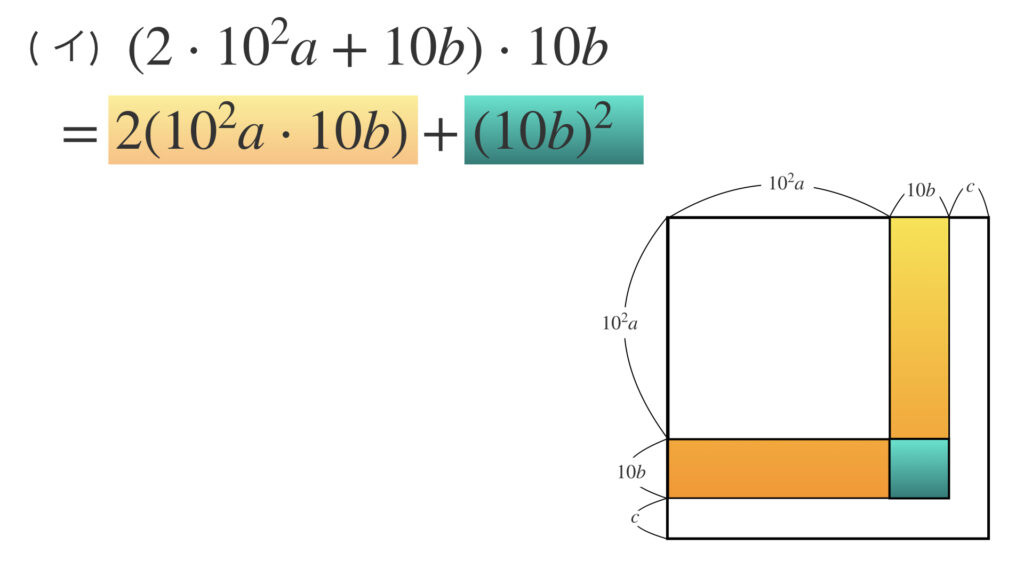
これは図のオレンジ青緑色の面積の和です。図を見ながらゆっくりと確認してみて下さい。
最後は(ウ)です。
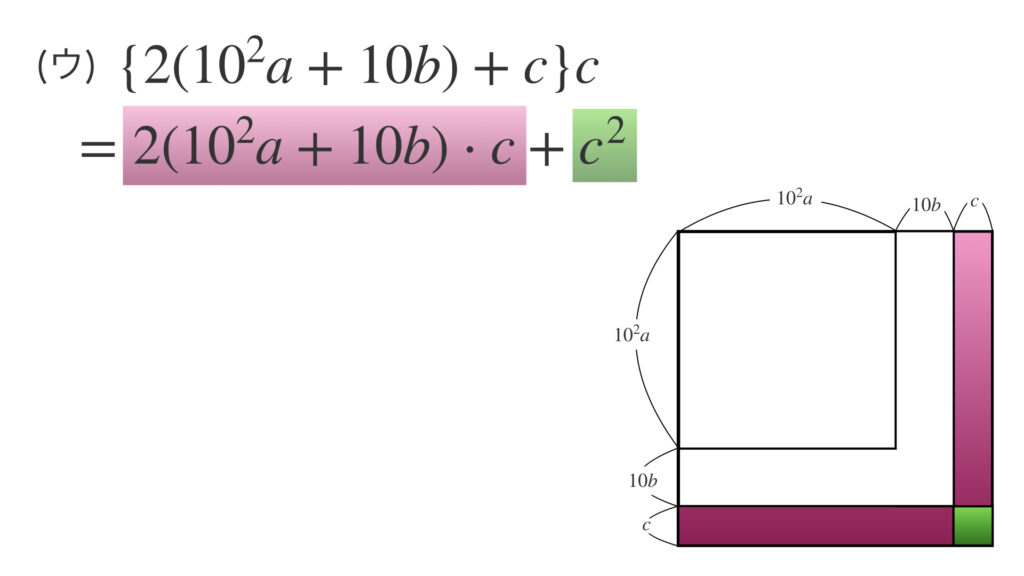
図の紫色と緑色の和です。
では $S=64516$ として $64516$ の平方根を求めたときの計算が何をやっていたのか確認してみましょう。
最初は(ア)より、10の位と1の位が0である3桁の数で、その数を2乗して $64516$ 以下で $64516$ にもっとも近い数を求めていたのです。すると100の位の数 $a$ が $2$ だと分かります。
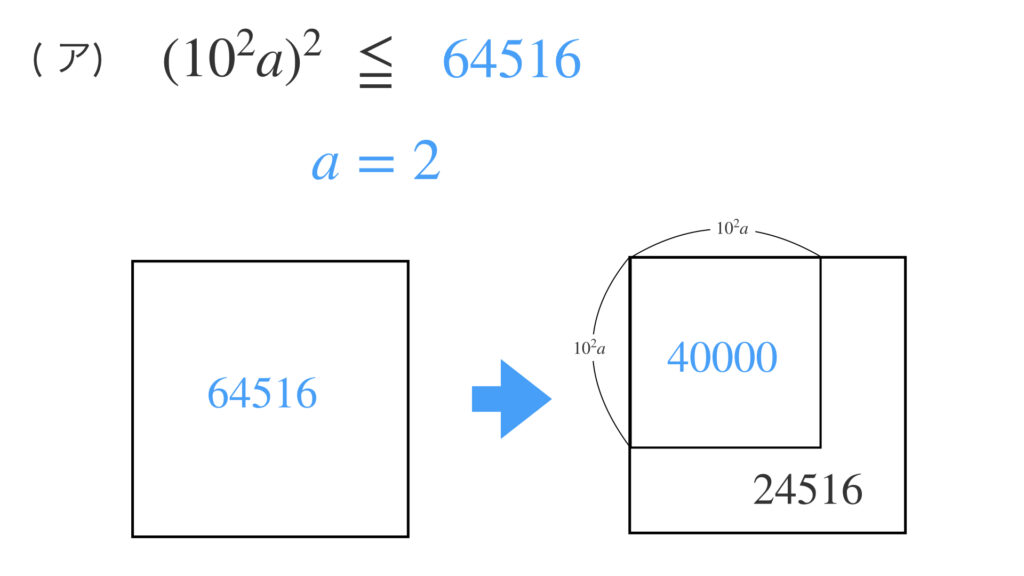
これを縦の計算では次のように書いています。
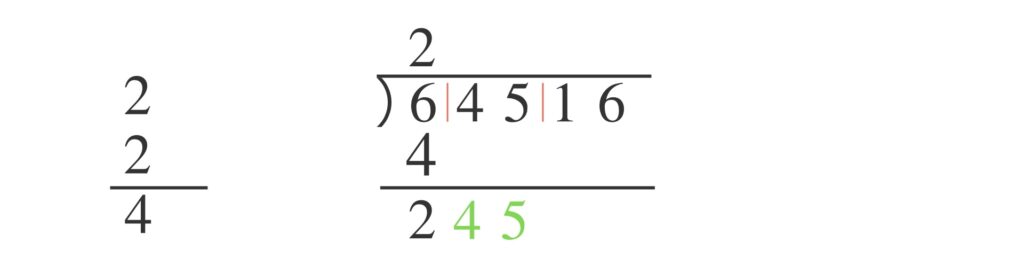
次に(イ)の式に $a=2$ として 次のような不等式を作ります。そして、この不等式が成り立つように最大の $b$ を求めます。$b=5$ と分かります。
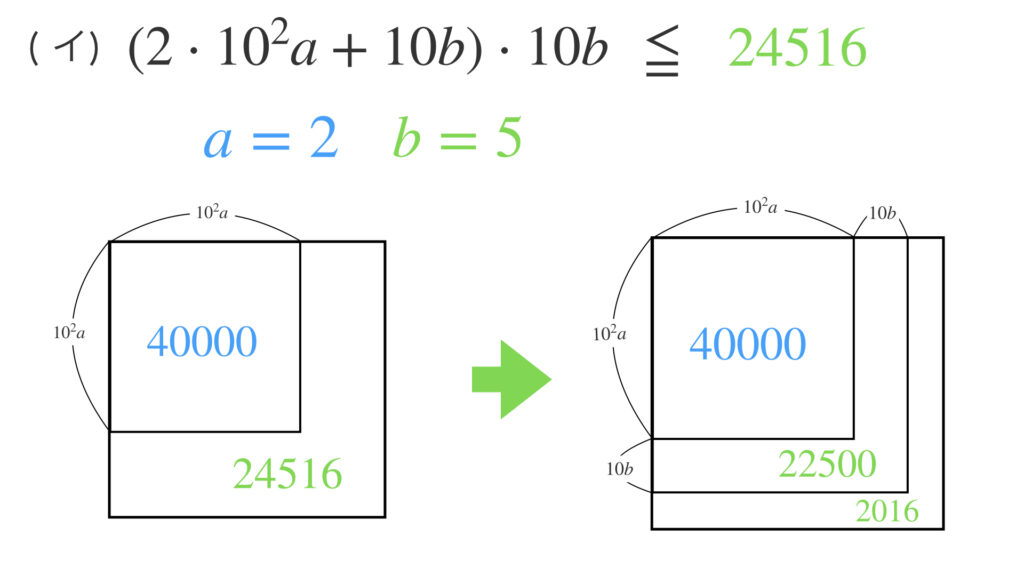
この $b$ を求めるために縦の計算では次のように書いていました。
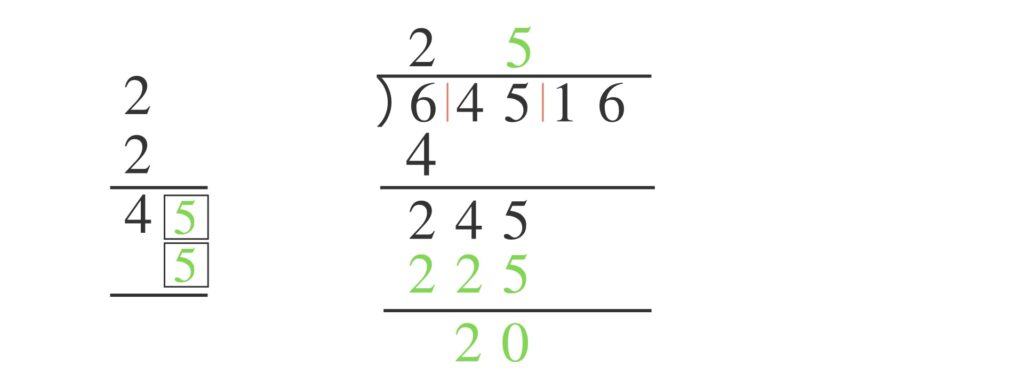
これを不等式と正方形の面積に照らし合わせて考えてみて下さい。
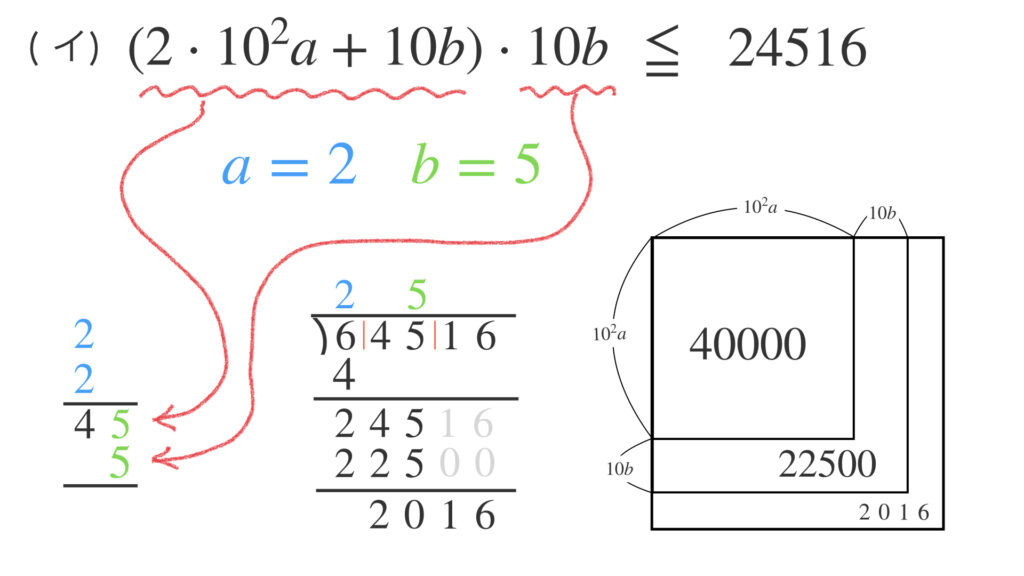
つまりこの不等式を解くために縦の計算をしていたのです。
最後に(ウ)の式に $a=2, b=5$ として次のように等式を作ります。そして、この等式が成り立つように最大の $c$ を求めます。$c=4$ だと分かります。
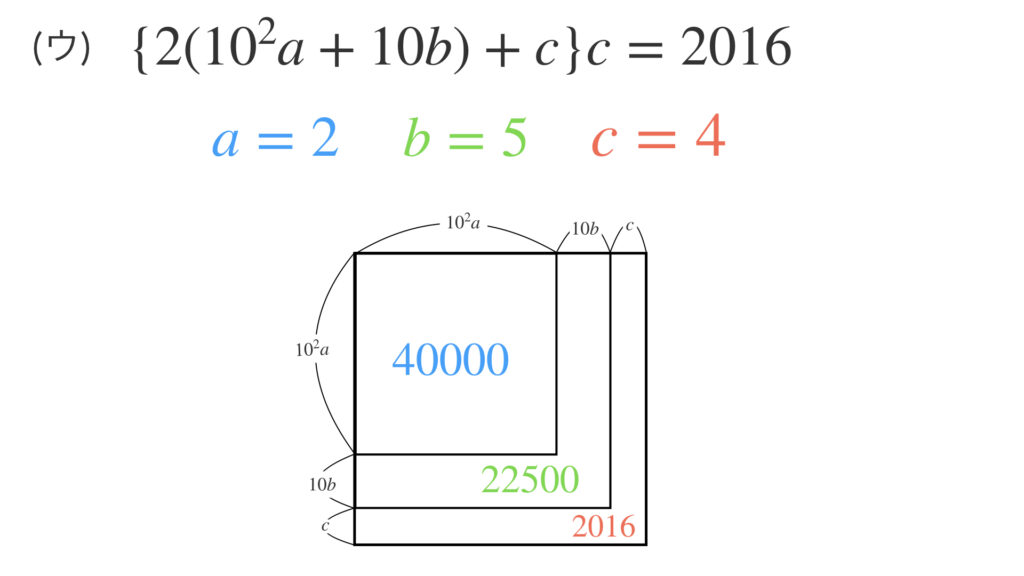
この $c$ を求めるために縦の計算では次のように書いています。

さっきと同じように等式と正方形の面積を見比べましょう。
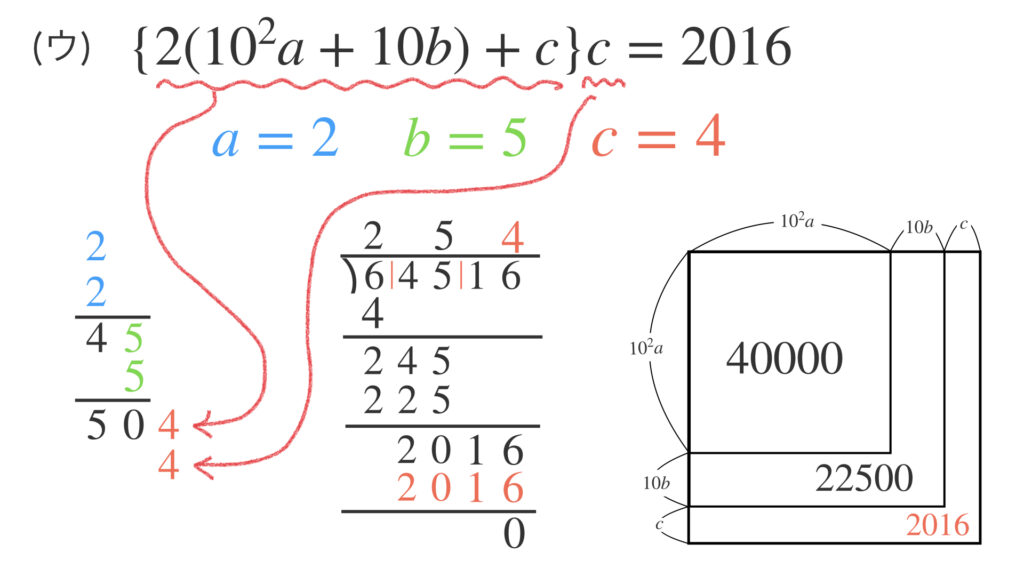
このように、等式が成り立つように $c$ の値を決めていたのです。
まとめ
平方根を求めるには、現在では計算機があるので「開平」を使う機会はありません。
しかし計算機を使えない場面で、開平を知っていたから助かったという時があるかもしれません。
大学入学共通テストが導入された影響で、数学の問題は「解ければいい」とされてきたものが「どうして解けるのか」を考えさせるようになりました。
「開平」の仕組みも基本的な計算の組み合わせで出来ています。
これはただの個人的な感想なので無視してもらって構いませんが、そのうち「開平」の仕組みが共通テストに登場するのでは、と密かに予想しています。たぶんその予想は外れるでしょうが、しかし少なくとも開平に限らず「解ける仕組み」を考える力は共通テストでは必須なものとなっていくでしょう。
 家庭教師の想い
家庭教師の想い 

