【三角関数】グラフの描き方がわからない！逆転の発想で描きやすくしよう！

一般的に関数のグラフを描く場合、最初に座標軸を描きますね。でも、この座標軸を先に描いてしまうと、グラフを描くのに窮屈な思いをする事ってありませんか？

グラフの形がわかっている場合には、グラフの概略を描いた後に座標軸を描いた方が簡単な場合があります。グラフを描くとき、かならず座標軸を先に描かなければならないという先入観を捨てましょう。

【スタディサプリ】動画授業で苦手を克服

関数のグラフの平行移動について

グラフを描くときグラフの平行移動の理解は大切です。グラフの平行移動の公式を確認しておきましょう。

もちろんこれは三角関数でも成り立ちます。この平行移動は、関数のグラフと座標軸の相対的な位置関係の変化ですね。一般的には座標軸を固定してグラフの方を移動させますが、関数のグラフを固定しておいて座標軸の方を反対方向に平行移動させても同じ結果が得られます。この原理を利用すれば、グラフが描きやすくなる場面が多くあります。

y = sin x のグラフを座標軸から描く

y = sin x のグラフは次のようになりますね。

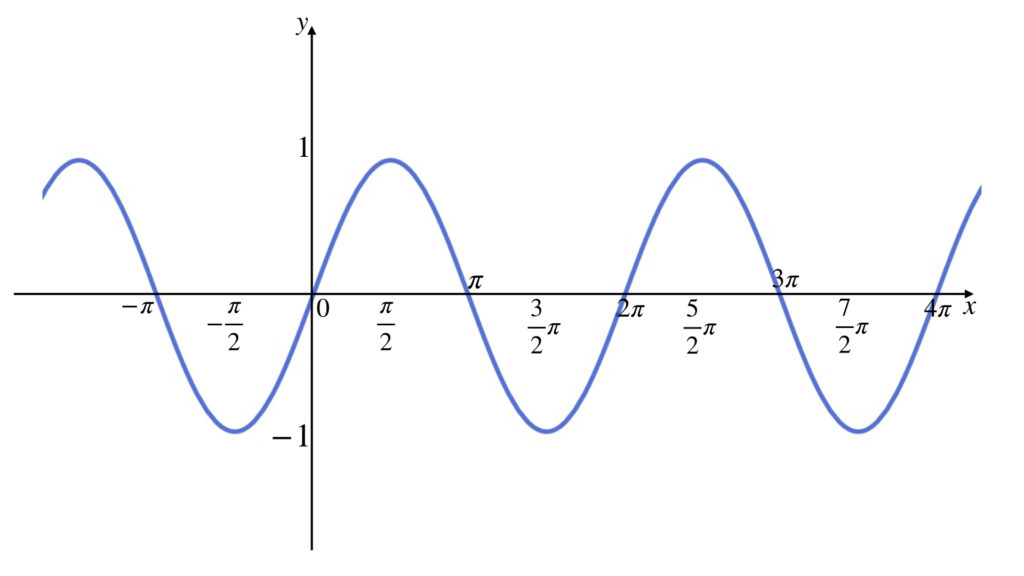
もし、これを座標軸から描けば、数値を座標軸に沿って等間隔に記入し、その値に対して y = sin x の値を点でとって、それらをなめらかに結ぶという手順を踏むことになります。

でも実際には、それほど厳密に描く必要がない場合が多いのです。そこで次のように描けば十分要求に応えられるグラフの概形が描けます。

y = sin x のグラフの効率の良い描き方

❶ x 軸と y 軸を描く。このとき軸上に数値は入れない

平行移動していない場合は座標軸から描いても構いません。しかし座標軸上には数値を入れないでおきます。

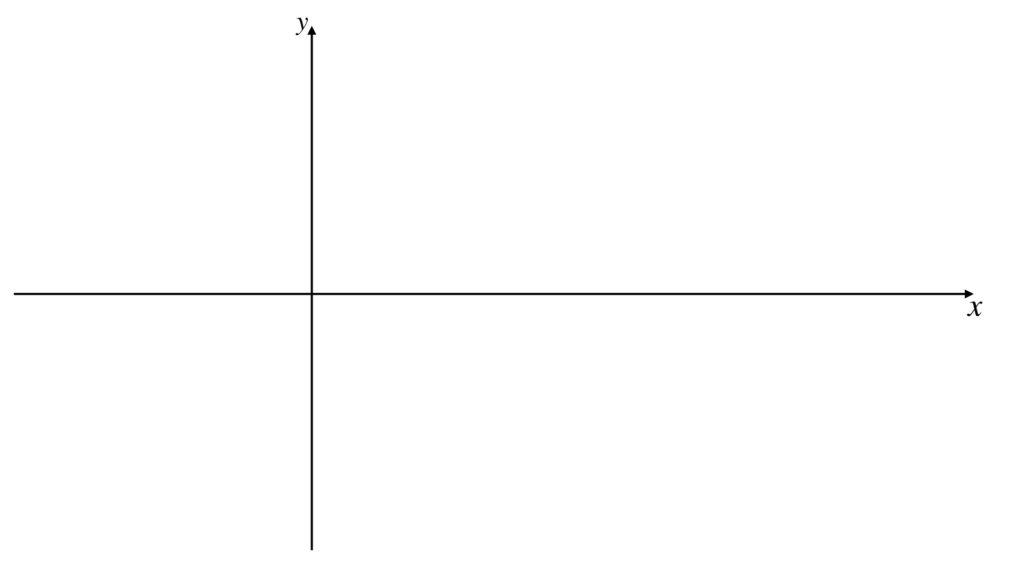
❷ グラフの概略を描く

サインカーブを原点から x 軸の正の方向に向かって、山→谷→山となるように描きます。このとき少しぐらい歪んでしまっても気にしません。

❸ 座標軸に数値を入れる

y = sin x のグラフは周期が 2π 、振幅が１であることに注意して座標軸に数値を書き入れます。

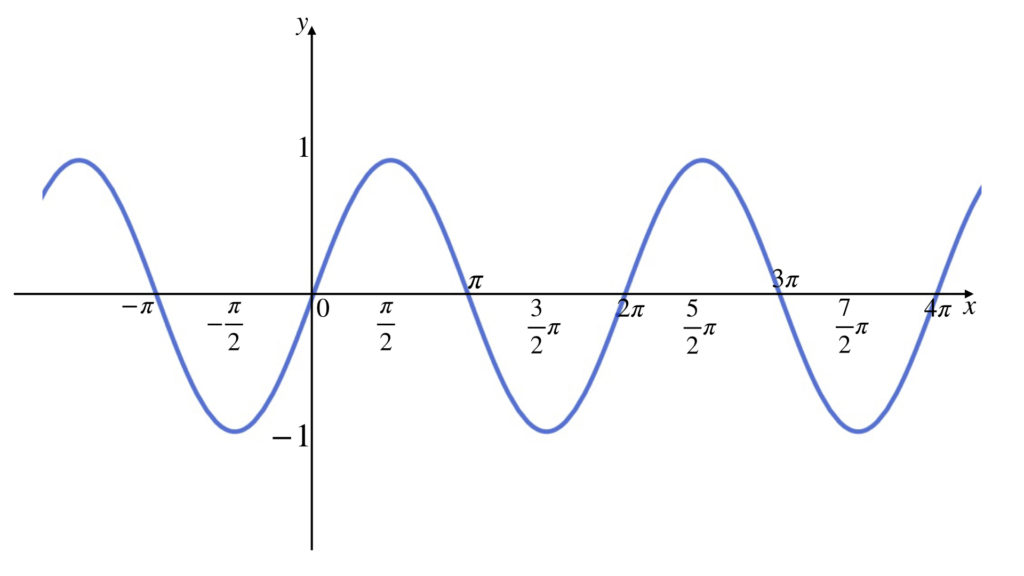
これで y = sin x のグラフが描けました。ポイントは座標軸に数値を入れるのを最後にすれば、グラフの概形に沿って入れればいいので、正確に描こうとする手間がいらないことです。

y = sin 2x のグラフの描き方

今度は y = sin 2x のグラフです。

❶ x 軸と y 軸を描く。このとき軸上に数値は入れない

平行移動はしていないので座標軸から描いても構いません。しかし座標軸上には数値を入れないでおきます。

❷ グラフの概略を描く

ここまでは y = sin x のグラフを描いたときとまったく同じです。下の図のようになります。

❸ 座標軸に数値を入れる

y = sin 2x のグラフのグラフは、周期が π 、振幅が１であることに注意して座標軸に数値を書き入れます。

つまり y = sin 2x のグラフは y = sin x のグラフをそのまま描いて x 座標軸の値だけを変えればいいのです。

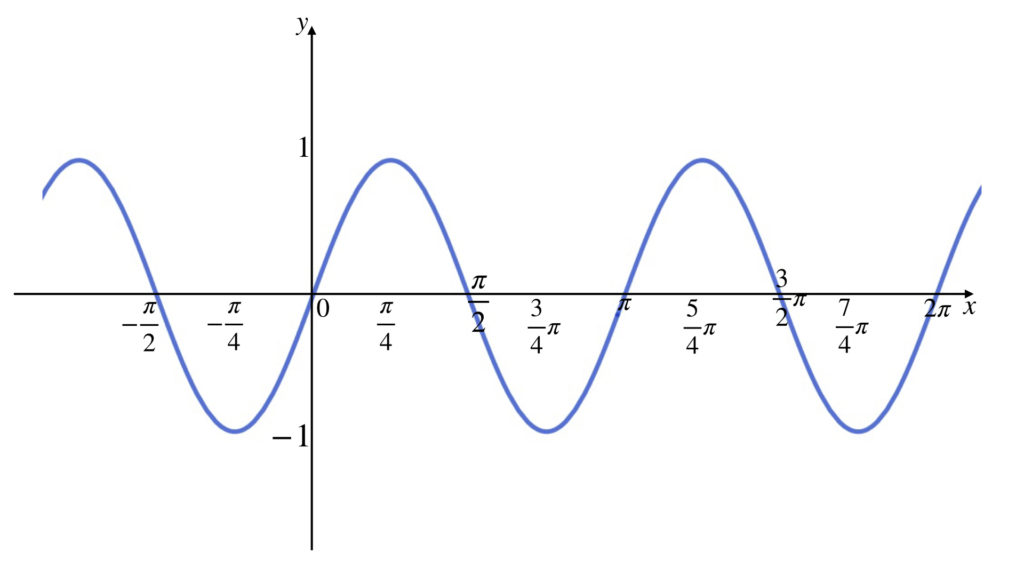
このとき座標軸に入れた値は y = sin x のグラフの値の全て２分の１になっていることに注意してください。

ですから、もし y = sin 3x のグラフを描きたければ、それらを３分の１にすればいいのです。y = sin x/2 のグラフなら２倍ですね。

y = sin x + 1/2 の描き方

❶ グラフの概略を描く

今回は平行移動があるのでグラフの概形から描き始めます。y = sin x のグラフを座標軸を入れずに描きます。正確でなくても構いません。

❷ y 座標を描く

x 軸方向には平行移動していないので y = sin x のグラフと同様の位置に y 軸を描きます。ただし数値は書き入れません。今回は y = sin x のグラフの概略から描き始めましたが、今回はy 軸から描いても構いません。臨機応変に進めましょう。

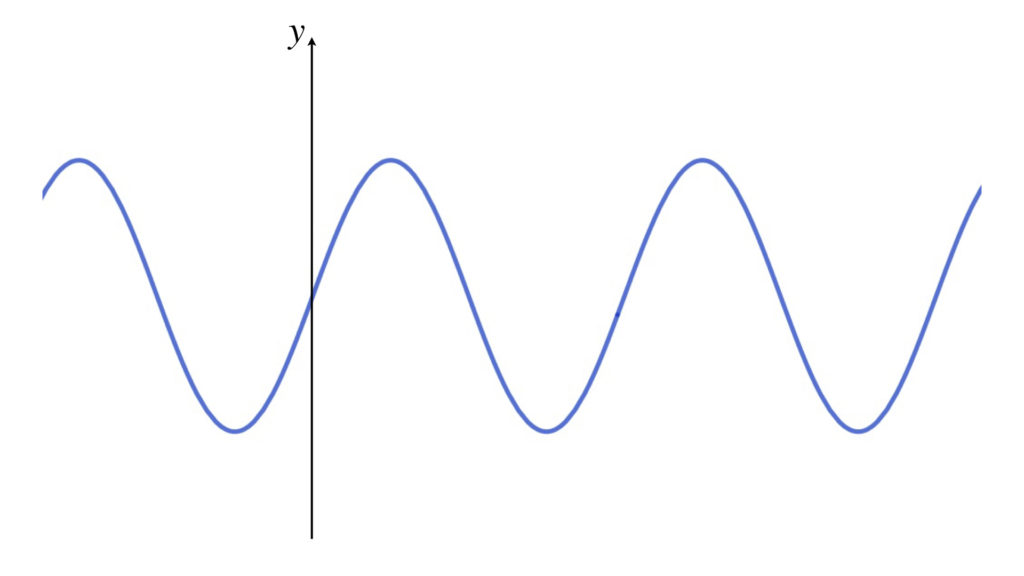
❸ x 座標を描く

y = sin x + 1/2 のグラフは y = sin x のグラフを y 軸方向に + 1/2 平行移動したものですが、それはグラフを固定しておいて x 軸を y 軸方向に -1/2 平行移動させたものと同じです。ですからグラフの概形は固定しているものとして x 軸を下に 1/2 ずらせばいいのです。

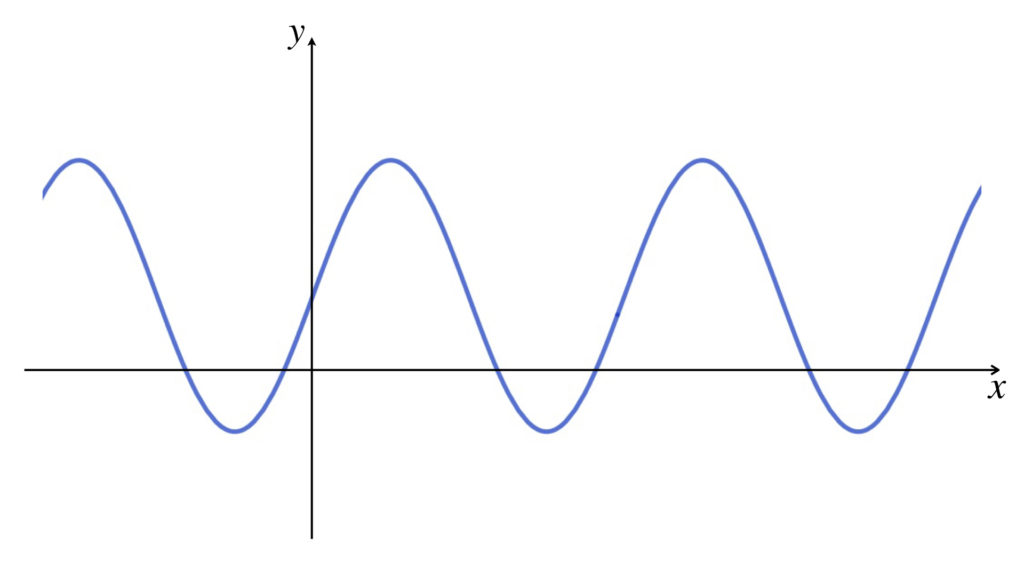
❹ 座標に値を書き込む

あとは座標軸に数値を書き入れるだけです。

x 軸上の数値は y = sin x のときと変わりません。つまり、x 軸を下に 1/2 ずらせば完成です。

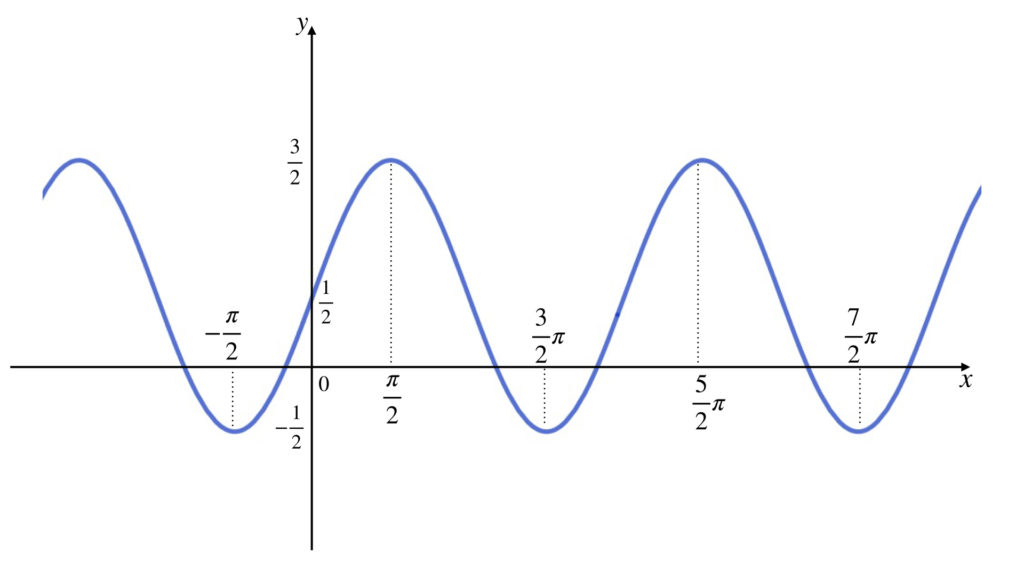
y = sin(x – π / 6) のグラフの描き方

❶ x 座標を描く

今回はy 軸方向には平行移動していないので、x 軸から描いても構いません。

❷ グラフの概略を描く

x 軸から描けば、グラフの概形を描くのに少しだけ楽になります。概形から描いても構いません。

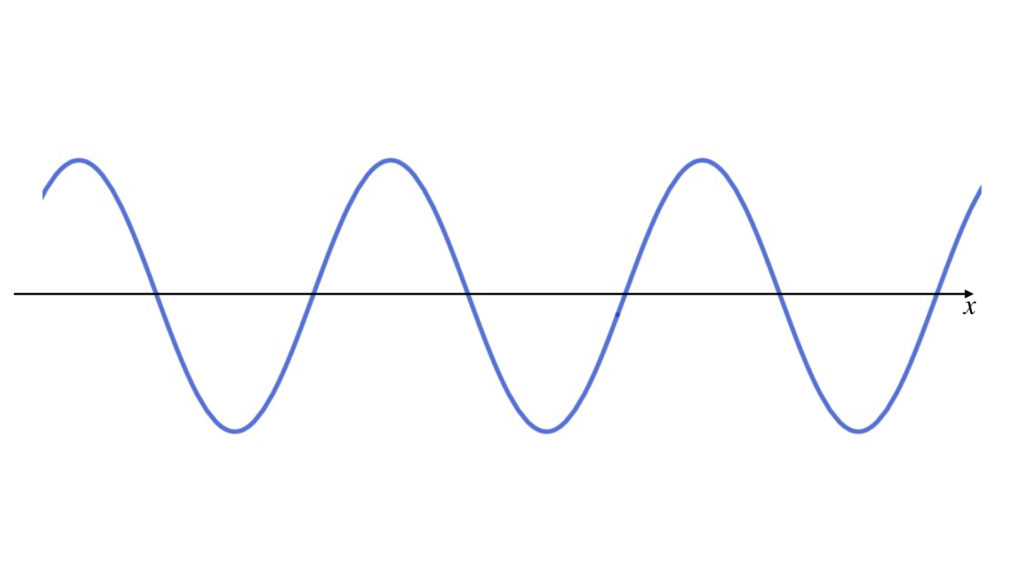
❸ y 座標を描く

y 軸を描き入れる位置を考えます。もう一度、平行移動について確認しましょう。

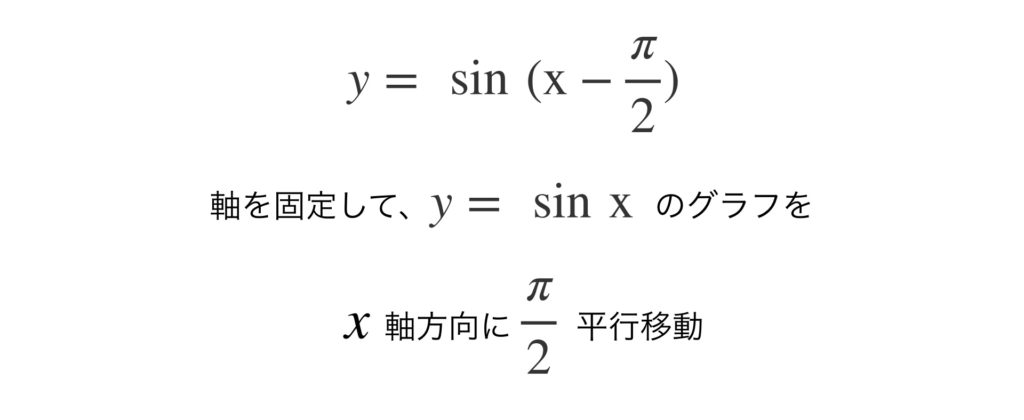
これを次のように読み換えます。

よって y 軸は次のようになります。

グラフの概形は動かさずに y軸の方をx軸方向に -π/2 ずらせばいいのです。

❹ 座標に値を書き込む

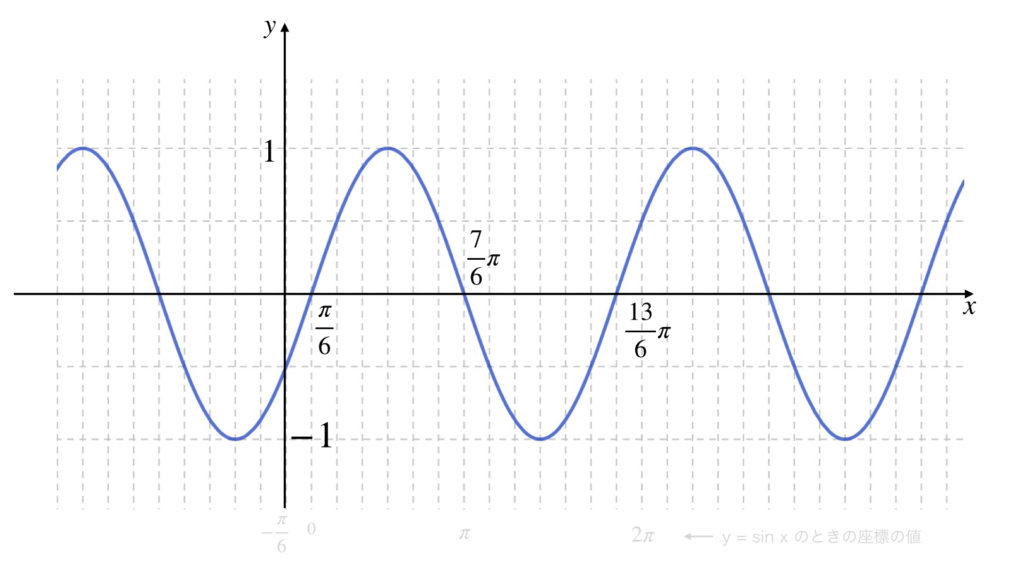
軸上に数値を書き入れます。このとき y = sin x のグラフを描いたときの x 軸の値が全て π / 6 を足した数値になっていることに注意してください。

まとめ

このように関数のグラフ描くとき、軸とグラフの位置関係は相対的なものだと認識しましょう。グラフの概形がすでに分かっているときは、軸とグラフを描く順番は臨機応変に決めてもいいのです。