ベクトルで、わからなくなってしまうポイントのひとつは「内積」です。
ただの「積」なら「掛け算」の意味ですが、なぜ「内」がつくのか、「内積」があるのなら「外積」もあるのか(実際「外積」もあります)、もし掛け算なら、矢印同士(ベクトル同士)を掛け合わせるってどういう意味があるのか、など今までの知識を駆使して、あれこれ考えてしまいます。
数学に限らず、わからないものに出くわしたら、それがわかるまでずっと考え続けるのものひとつの道ですが、とりあえずわかったことにして先に進んでみるのも挫折しないためには良い方法です。
このベクトルの「内積」というのも、その意味を納得するまで考えようとすると「わかったような、わからないような」状態に陥ってしまいます。最初から理屈を掘り下げるよりも「とりあえずわかったことにしてみる」方が理解がスムーズに進むときだってあります。
目次
ベクトルの内積の定義
「定義」とは、用語の意味を他の用語と明確に区別できるように、たったひとつの説明で限定したものです。
ですから「内積」という用語も、他とは区別して、そのものだけを受け入れる必要があります。
「積」という言葉が入っているからと言って「掛け算」との関係を考える必要さえありません。他との関係性で内積を理解しようとすると逆にわからなくなってしまうのです。
定義の通りに「そうゆうもの」と受け入れてしまって、受け入れた後に現れてくる事実に着目してみましょう。その方がうまくいくときがあります。これは内積ばかりではなく、数学を効率的に理解するコツでもあるのです。
では、その内積ですが、次のように定義されています。具体的に見ていきましょう。次のふたつのベクトルを考えてください。

このふたつのベクトルを平行移動して矢印の出発点が重なるように連結します。

このとき半直線OAと半直線OBのなす角をθ とします。するとふたつのベクトルの内積は次のように表します。ベクトルとベクトルの間の「・」が内積を意味します。
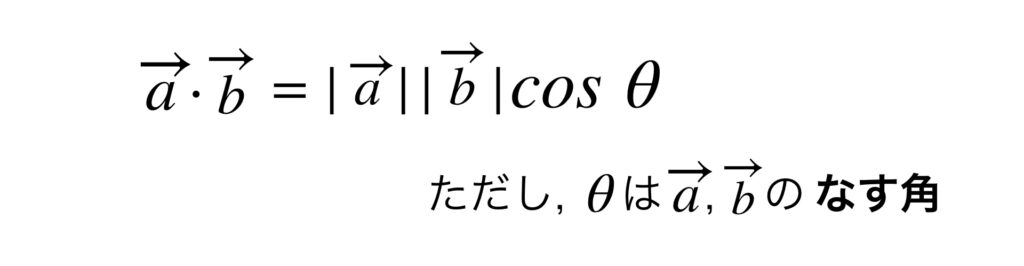
それでは、この定義から導き出される事実とは何なのでしょうか?わかることをひとつひとつ確認していきます。
ベクトルの内積の定義からわかること
① 内積はスカラー量である
内積の定義の式をよく眺めてください。すると内積はベクトル量ではなく、スカラー量であることがわかります。すなわち、実数値だけで方向は関係ありません。

② ベクトルが同じ向きの場合
ベクトルが同じ向きのとき、すなわち、なす角が0度の場合を見てみましょう。例えば、次のような場合です。

内積を計算してみます。
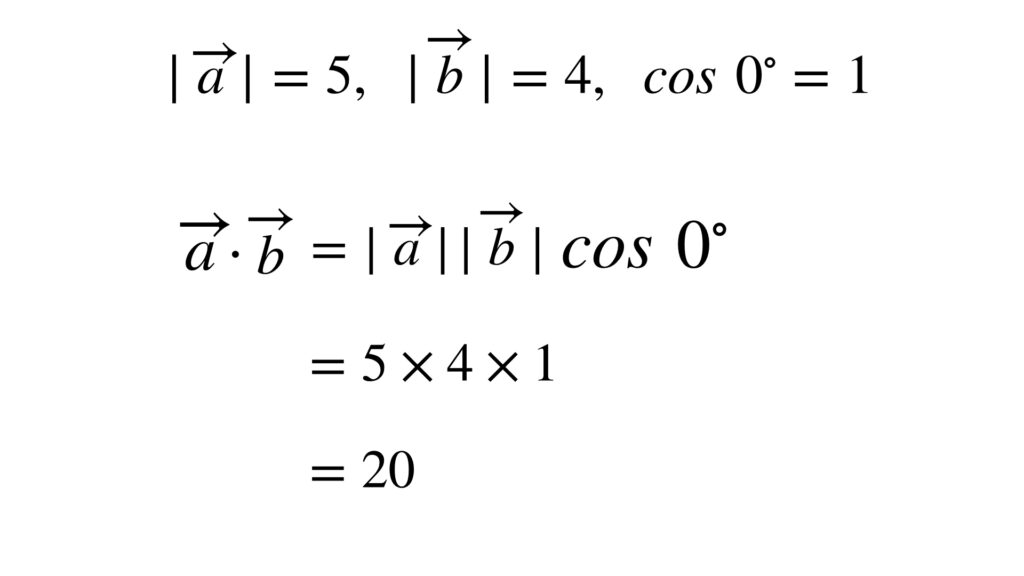
これは原点からのそれぞれの位置ベクトルが示す数直線上の数値を掛けた値と一致しています。
同じ向きのベクトルの内積は、それぞれの大きさを掛けた値になるということですね。
特に、全く同じベクトルの内積を考えると次のことがわかります。大きさが5で同じ向きのベクトルを使って具体的に計算してみます。
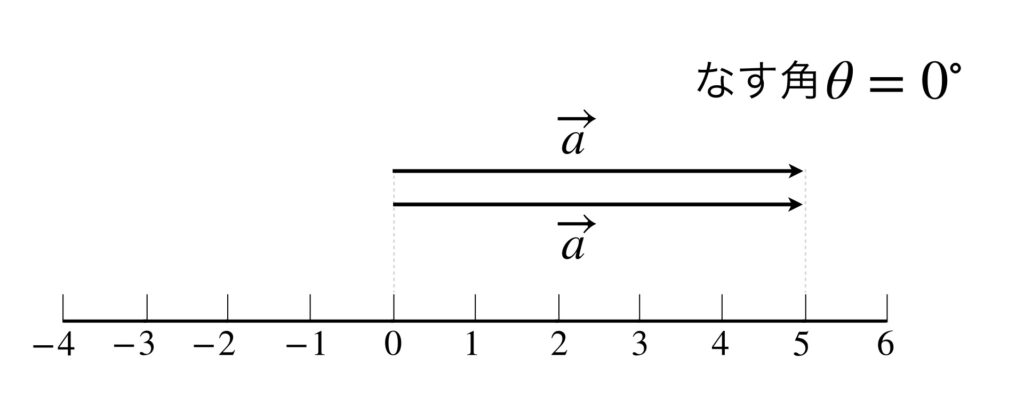

これから内積の性質として次の式が成り立ちます。
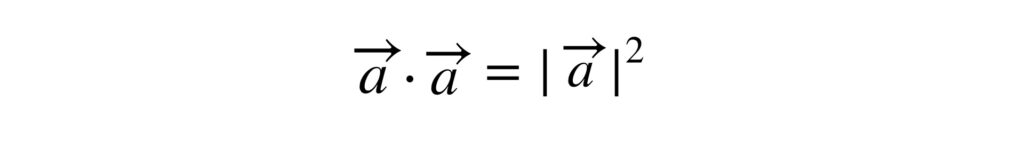
同じベクトルの同士の内積は、そのベクトルの大きさの2乗と同じ値になるということですね。今後ベクトルの計算を考えて行くとき、この性質はとても重要です。
③ ベクトルが反対向きの場合
ベクトルが反対向きの場合、すなわち、なす角が180度の場合を見てみましょう。例えば、次のような場合です。
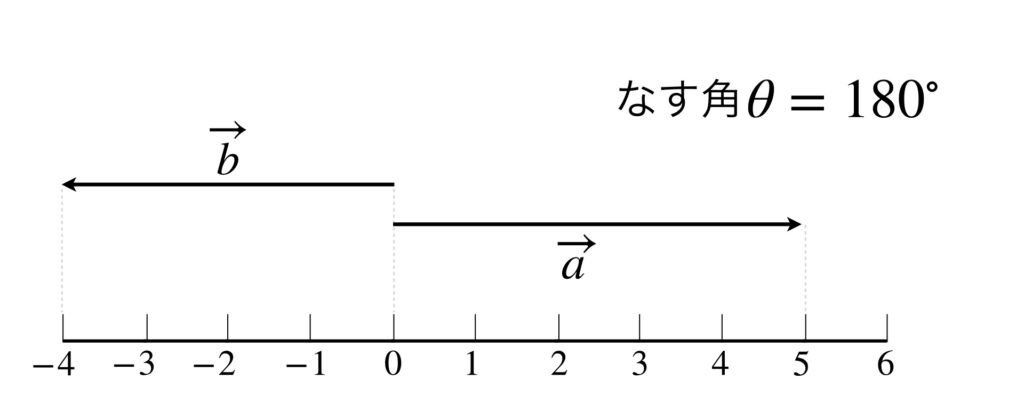
ベクトルの定義に従って計算すると次のようになります。
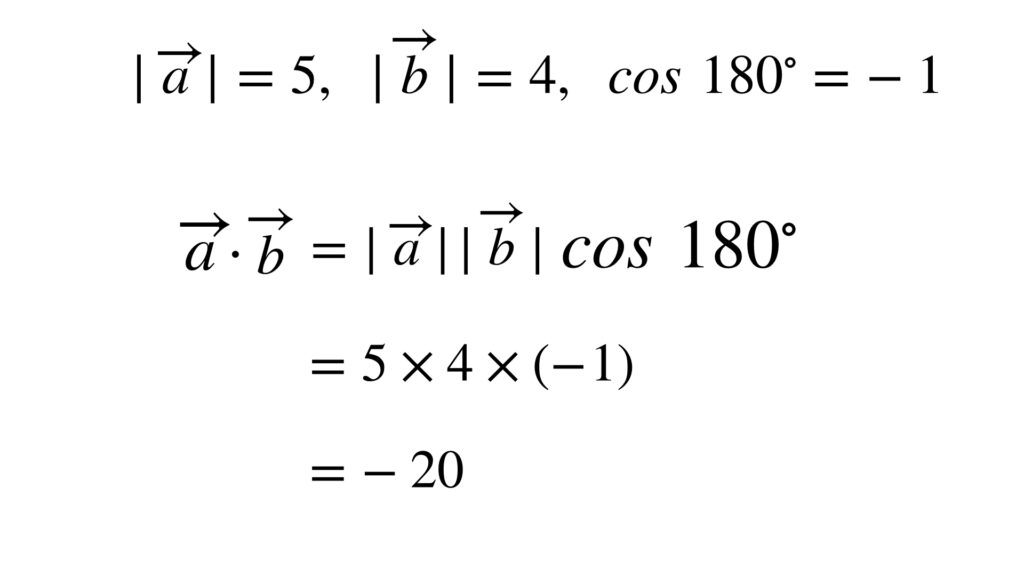
これも原点からのそれぞれの位置ベクトルが示す数直線上の数値を掛けた値と一致していますが、出てきた数値は負になります。
②と③からわかること
上記の②と③で次のことがわかります。つまり平行なベクトル同士の場合です。

内積の計算をして、それぞれのベクトルの大きさを掛けた値、またはその値にマイナスをつけた値なら、それらのベクトルは平行であることを意味しています。また、その逆も成り立ちます。正の値なら同じ方向で平行、負の値なら反対向きで平行です。
④ ベクトルが垂直の場合
次にベクトルが垂直の場合、すなわち、なす角が90度の場合を見てみましょう。例えば、次のような場合です。
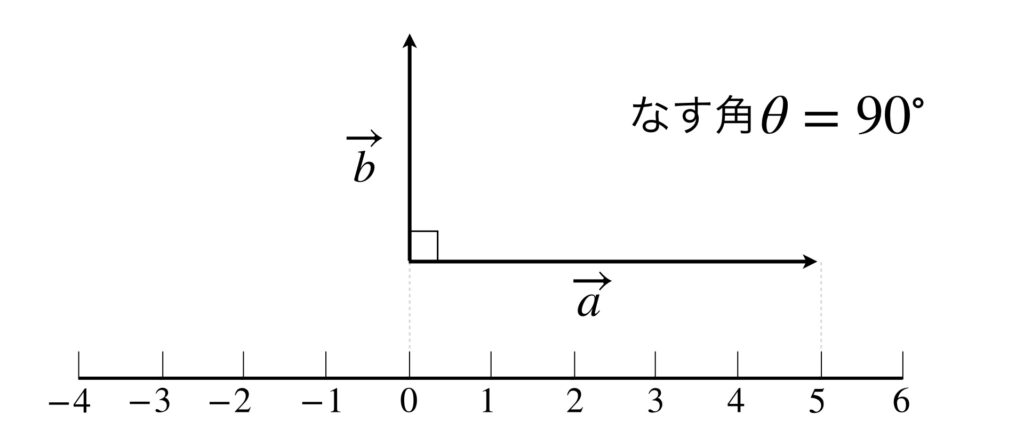
計算してみます。
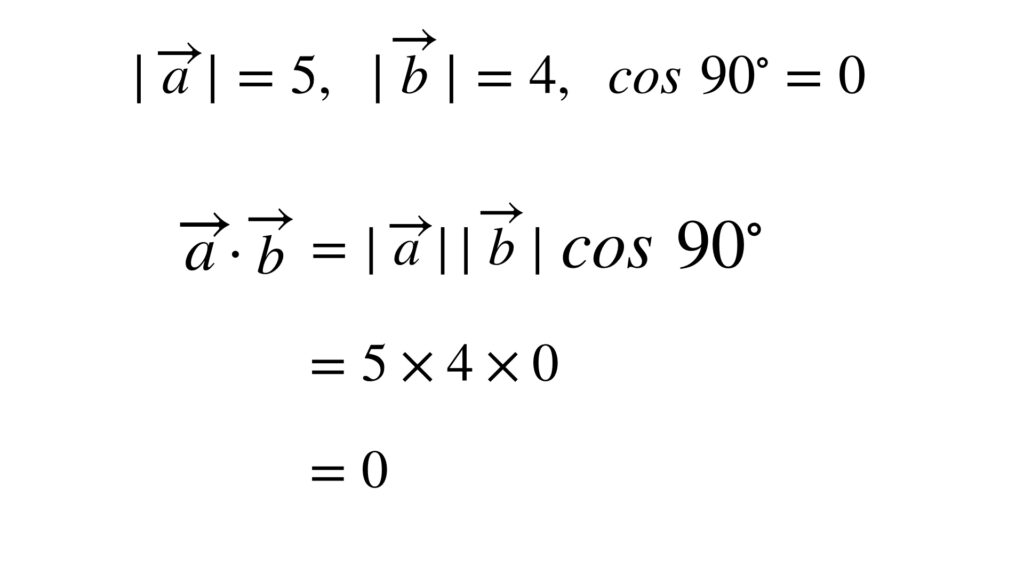
これによって次のことがわかります。

すなわち、共に零ベクトル(ゼロベクトル)でないふたつのベクトルの内積を計算した結果が0になる場合、そのふたつのベクトルは垂直です。これも逆が成り立ちます。
内積の定義から導き出される内積の性質
その他、内積の性質として次のようなことが成り立ちます。証明は省きますが、どれも納得しやすい内容です。それは文字式の掛け算から類推できる結果だからです。
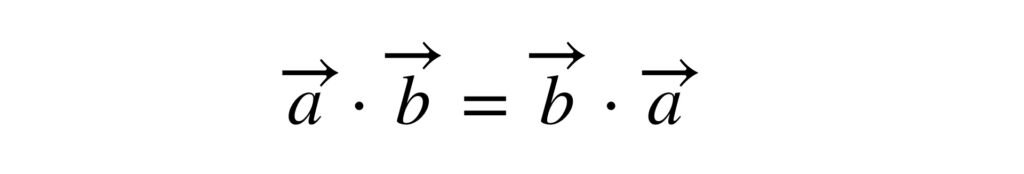

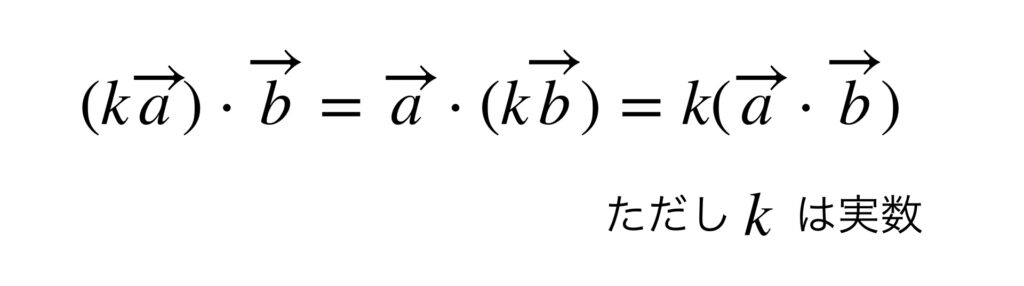
つまり、ベクトルの内積の計算では、交換法則や分配法則が成り立ちます。ただし内積は、ふたつのベクトル間についてのみ計算される値である点に注意してください。次のような計算はありません。

内積の計算
さて、上記の内積の定義と性質により、次のような計算が可能になります。
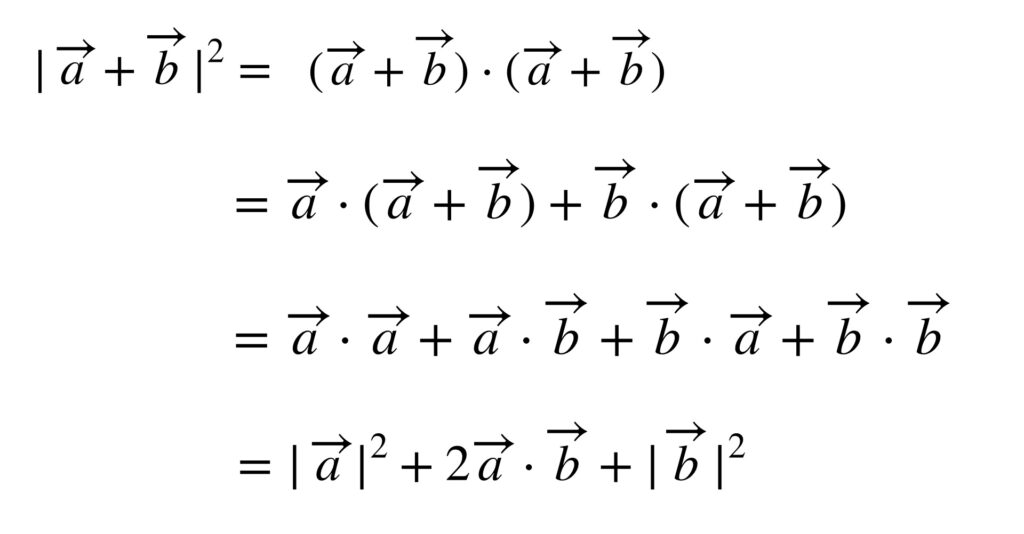
この結果は、よく知っている展開公式に似ていますね。
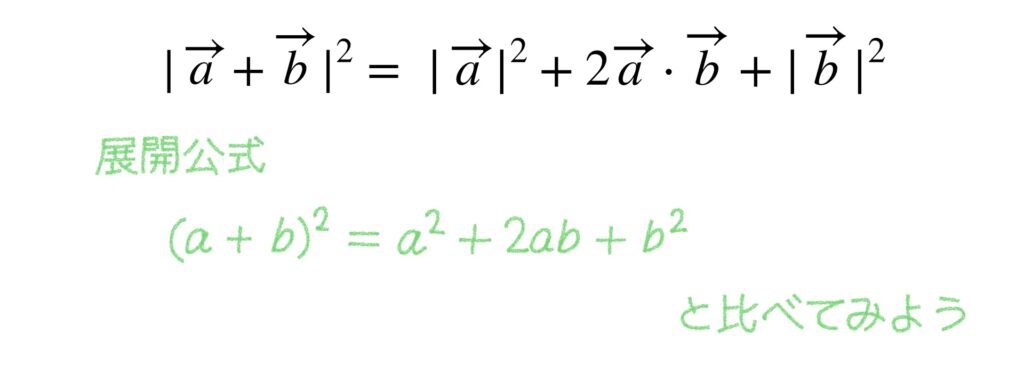
これはよく使うので公式として覚えてしまいましょう。
内積の計算の応用
では、このような内積の計算ができると、どのようなメリットがあるのでしょうか。次のような実際の問題を解いて実感しましょう。

今回は問題をイメージするために図も示しますが、ベクトルの計算に慣れてしまえば、図など描かなくても計算問題として答えを導き出せます。むしろ計算だけで解けるようにすることがベクトルを学ぶ目的のひとつです。
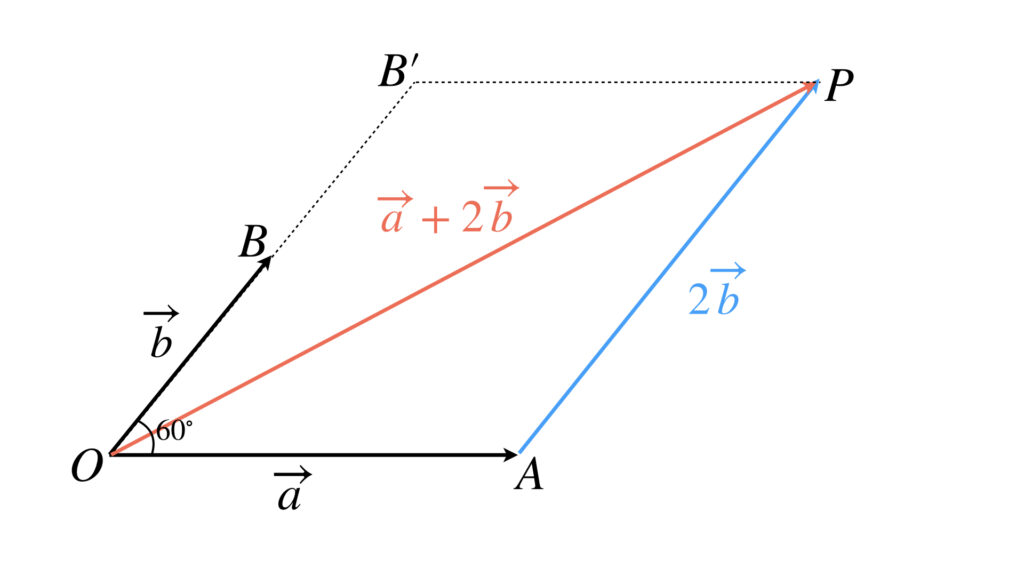
計算を始めます。求めたいベクトルの大きさを式にすれば次のようになります。
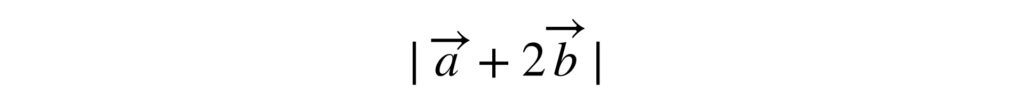
しかし、ここから始めると計算しにくい(公式が使いにくい)ので2乗にしておきます。あとで正の平方根を求めればいい(ルートを付ければいい)からです。
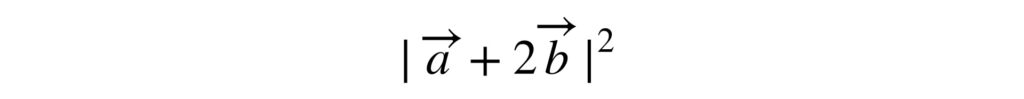
公式を使って次のように変形させます。
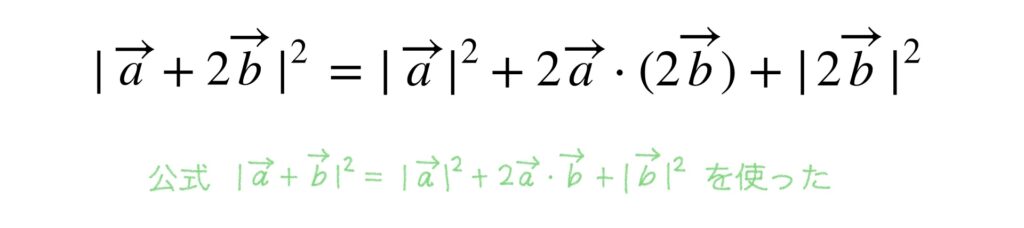
式を整理していきます。
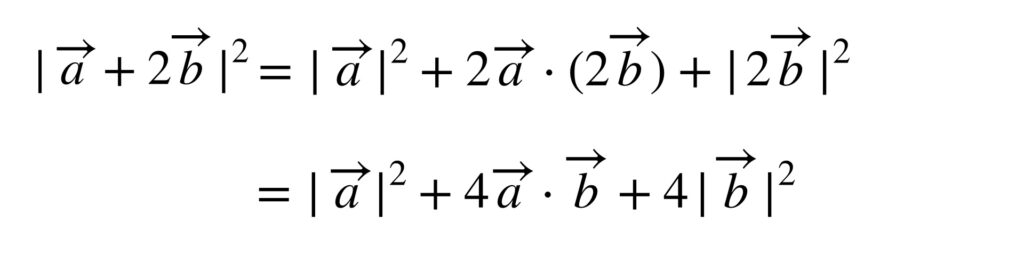
必要な値を確認しておきましょう。
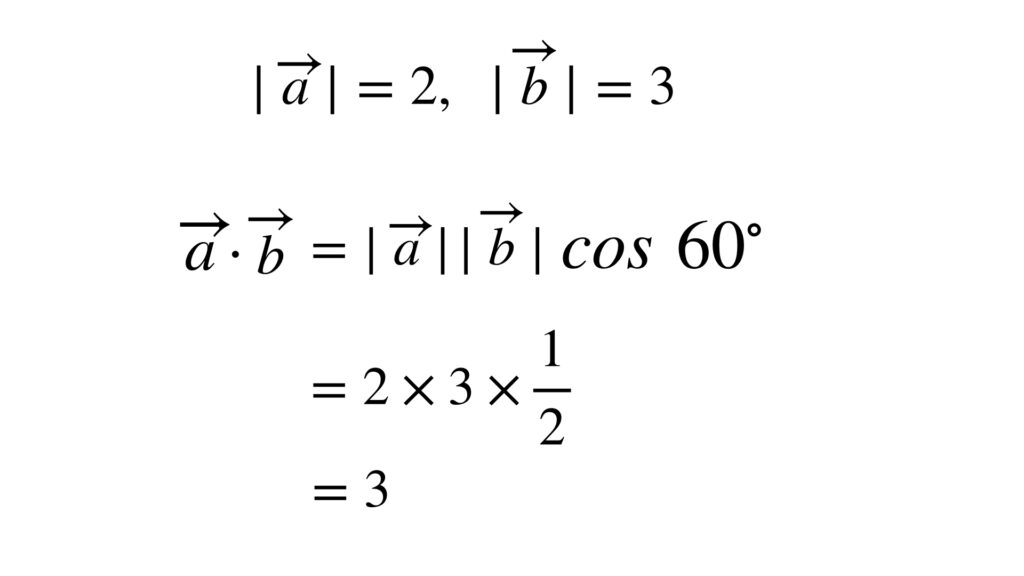
数値を代入して計算を続けます。
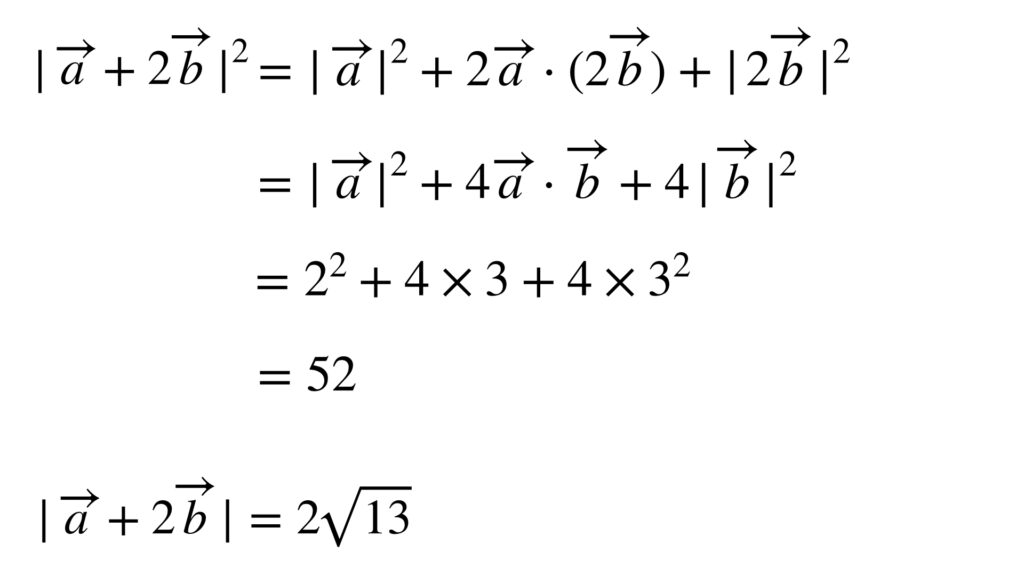
これで求まりました。ところで内積を使わず図形の性質を使っても同じ答えが得られます。しかしそのためには図を描き、そこから適用できる図形の性質を導き出さなければなりません。その場合はどのように解くのか、図を見てもう一度考えてみましょう。

解法が思いつきますか?どうやら余弦定理が使えそうです。
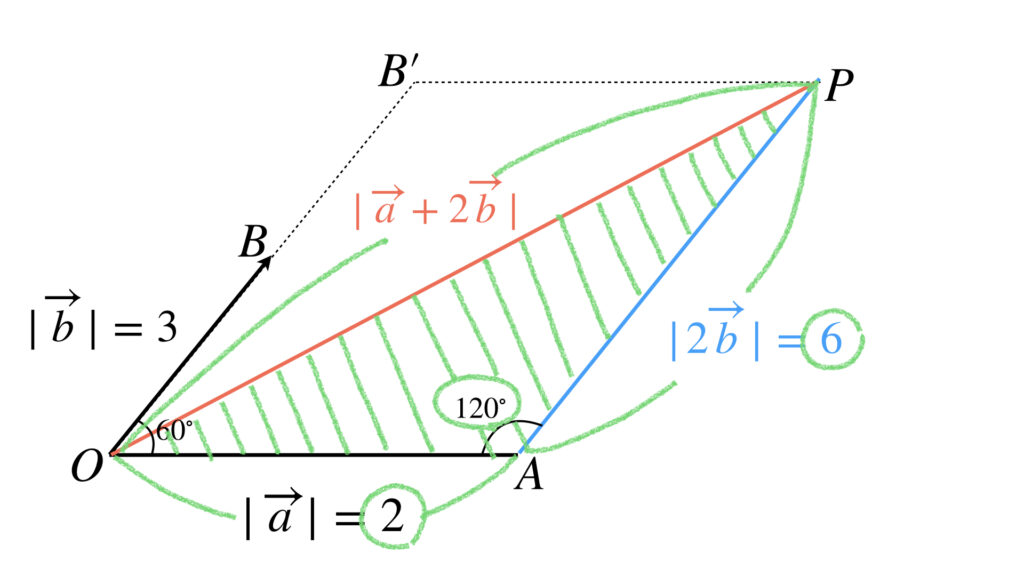
三角形OAPに余弦定理を適用します。計算は次のようになります。
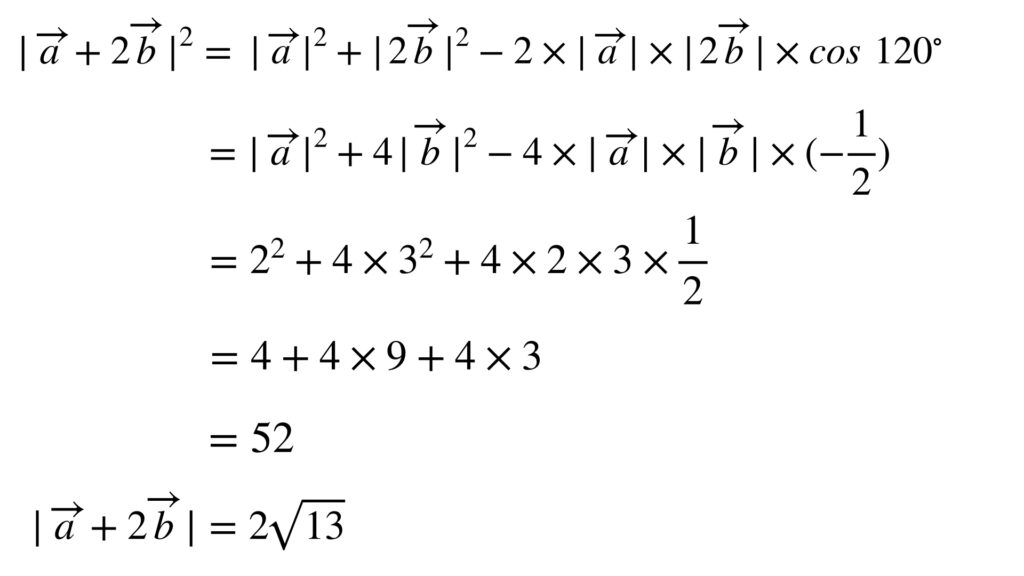
同じ答えが得られました。
図形問題が得意な人なら余弦定理の適用を思いつくのは、それほど難しくないかもしれません。しかし図形に慣れていないと、それを思いつくのはたいへんです。
ベクトルの解法は計算の手順さえ正しく行えば正解が得られます。図形問題が計算で求まります。
ベクトルってすごいと思いませんか?
 家庭教師の想い
家庭教師の想い 

