生徒さんを教えていて「どうしてこんなに簡単なことが分からないのだろう」と悩むことがあります。どうやったらこれ以上わかりやすくできるのか、こちらが悩んでしまうほど基本的なものだと教えるのに困ってしまうのです。
目次
わかったけれど、わかっていない
いえ、生徒さんは「わかった」と言ってくれるのですよ。
でもあとになって「ああ、わかっていなかったんだな」と気づくときがあり、だったら最初から「わからない」と言ってくれたらいいのにと思うのですが、でも「わかった」と言ってくれたそのときには、生徒さんは、決してウソをついたのではなく、本当に「わかった」と思って言っているのですね。
どうしてわかったの?
それとは逆に、どうしてそこで分かってしまうのか、あまりにも速すぎる理解にこちらの方が戸惑ってしまうときもあります。
この程度の説明で分かってしまうがずがないのに、と思って試しに問題を解かせてみると、案の定、生徒さんは思いもよらない方向に考えを進めているのです。その間違いを指摘して正しい方向に修正するのに随分と手こずることもしばしばです。
「分かる」って一体なんなのでしょうね。
教える側の「分かる」と教わる側の「分かる」には、少なからずギャップがあるのです。
わかるための前提条件
そもそも「分かる」とは、今までの知識を使って新しい知識を受け入れられるようになることですから、教えている子の今の知識がどのようなものか、教える側がしっかりと掴んでいないと、教えるための前提条件が整っていないことになります。
たとえば「『分速』とは、速さを1分間に進んだ道のりで表したものです」と教えたとしたら、その前提条件は、「速さ」「道のり」という言葉の概念と、なぜ1分間が適当なのか、その理由といったところになります。
この前提条件は、「もはやこの程度は知っているだろう」と教える側が無意識に設定しているので、それが生徒さんの知識と一致していなければ、生徒さんは表面的な理解は得られても、根本的な理解を得ることはできません。
「速さ」ってどうゆうこと?
生徒さんは「速さ」という言葉は知っています。でもそれが程度を表す言葉だと認識できているかどうかは確かめておく必要があります。
わたし「速さって何?」
生徒さん「道のり÷時間でしょ」
わたし「うん、その通りなんだけど、速さの意味を答えて欲しいんだ」
生徒さん「どうゆうこと?道のり÷時間で求まる値が速さじゃない?」
わたし「そうだよ。でも質問したいのは速さの計算のやり方ではなくて、その意味についてなんだけど」
生徒さん「どうゆうこと?質問の意味が分からない」
こんなやりとりがあれば、わたしが当然に答えてもらえると思っていた前提条件が決して当然ではなかったことに気付かされます。
わたしとしては、生徒さんは、どれだけ早いのか、または、どれだけ遅いのかの程度を数値で表したものが「速さ」だと認識できていると思っています。その認識がないとその後の説明が難しくなります。
そこで先ずは「速さ」という言葉の意味から確認していきます。「速い」の対義語は「遅い」で、この「速い」「遅い」を表すにはどうしたらいいのか考えてもらいます。
「歩くのと走るのは、どちらの方が速いでしょうか?」
この質問は、ほぼ間違いなく走る方と答えてくれるでしょう。もっとも競歩などを考えたら答えが正しいとは限らないのですが、実感を持ってもらうために身近な例で説明したいので、細かいことには目をつぶります。
「同じ10秒間なら、歩くのと走るのでは、どちらの方が遠くに行けるでしょうか?」
これも感覚的に走る方と答えるでしょう。
「ならば同じ時間でより遠くに行ける方が速いということだね」
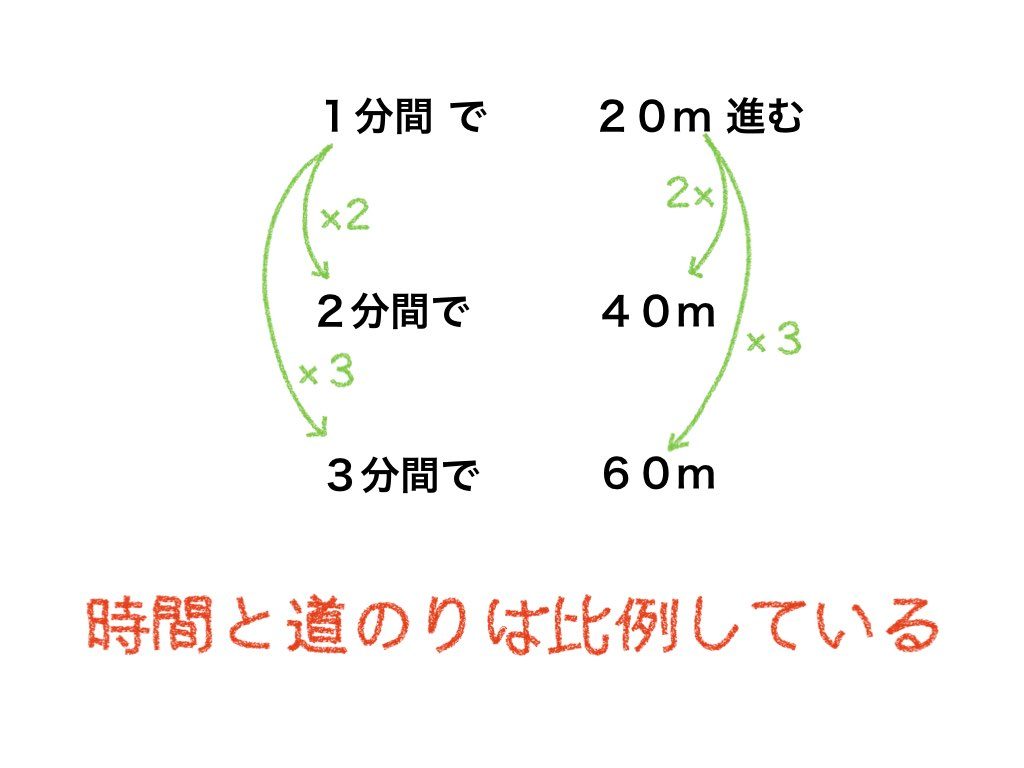
そして、なぜ1分間とか1時間とか、つまり単位時間で速さは表した方がいいのかを考えてもらいます。
このことについては解説するよりも生徒さん自身に考えてもらった方がいいかもしれません。もしそれがピンとこないようであれば比例の考え方を取り入れて解説することを試みます。
この理解ができてから速さの問題を解説していくと、とてもスムーズに運ぶようになります。
「わかった?」と訊いてはダメ!
このように、教師側が暗黙のうちに認識しているだろうと決め付けているものが生徒側になかったら、教師の「わかった?」と生徒の「うん、わかった!」には不一致が生じてしまいます。
それでわたしは、教えている最中に「わかった?」とは極力訊かないように心がけています。生徒さんに「うん、わかった!」と言われると、こちらが安心してしまい、教えそこなう危険がありますからね。
そして、できるだけ生徒さんの視点に立って教えるように努力しています。
でもこれが難しいのです。
 家庭教師の想い
家庭教師の想い 

