家庭教師の想い 
数列のわかりにくさには原因があります。
数列が苦手な人は、数列の問題を考えるとき、「順番」の話と「その値」の話が混じり合ってしまうのです。
それをはっきりと分離して考えることができれば数列の問題の見通しがよくなりますよ。
目次
数列の具体例で考える
数列の「順番」と「その値」がどのようなものか具体的に説明します。
次のような問題を考えてみましょう。
この問題が直感的に把握できるように図にしてみます。
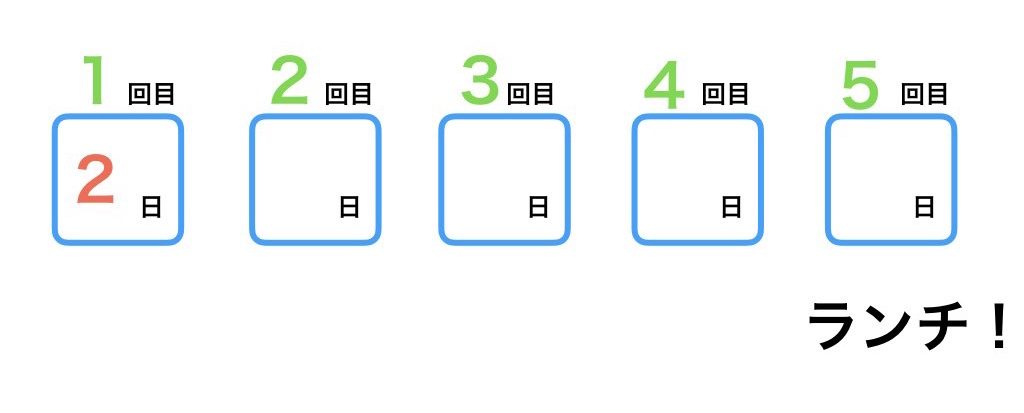
何を考えればいいのか分かるようになりましたね。
３日おきに配達してくれるのですから最初の日から順々に３を足していけば配達される日がわかるはずです。
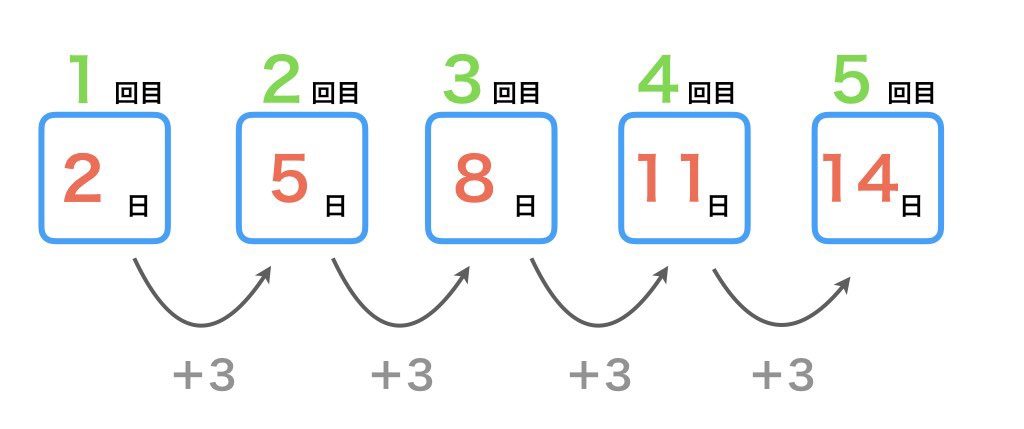
これでランチの予定は１４日に入れればいいとわかりました。
これでは小学生の簡単な問題ですが、「順番」と「その値」をしっかり分離して理解してほしいので、あえて説明しています。
数列が得意な人から見れば、こんなこと当たり前だと思うでしょう。しかし数列が苦手な人は、「順番」と「その値」が分離できていないのです。
数列の「順番」と「その値」の関係
では、「順番」と「その値」の関係をもっと明らかにしていきましょう。
「順番」とは配達の回数のことです。そして「その値」とはカレンダーの日付です。次の図で確認してください。
「順番」の初期値が１回目であり、「その値」の初期値が２日です。
そして、その日から３日おきに次の配達日が訪れるので、２回目の配達日、３回目の配達日が分かります。
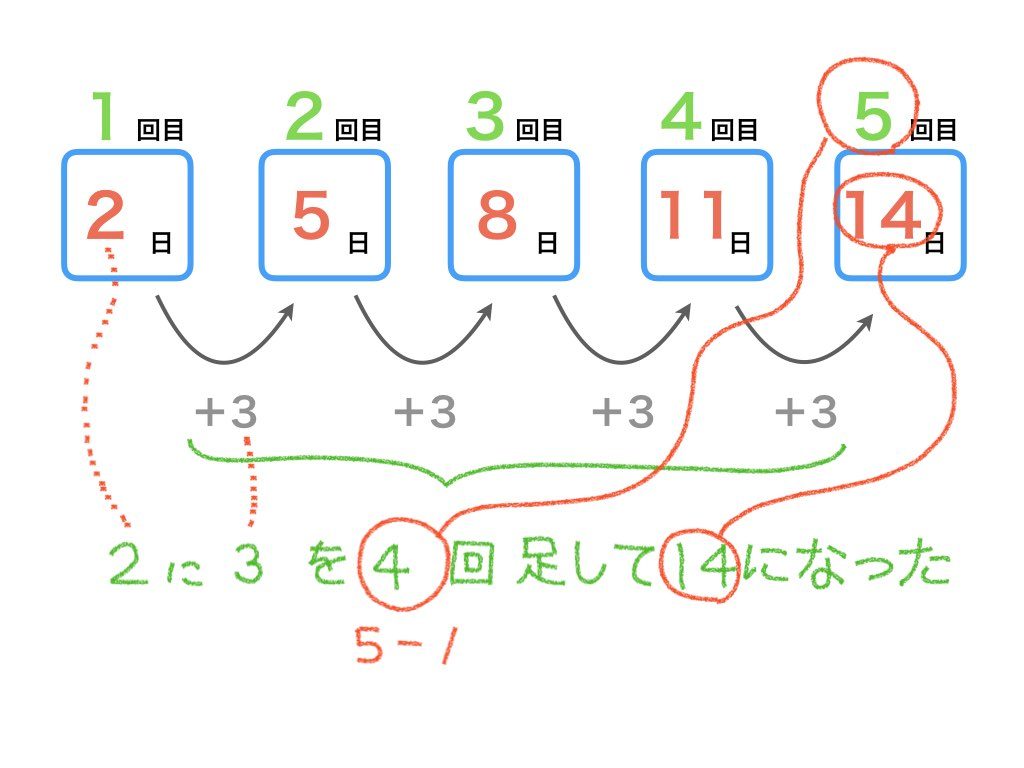
最初の日がわかれば、それに３を何回足したらいいのかわかればいいのですね。
これが分かれば何回目でも ( 今回は月をまたげないので限界がありますが ) そのが何日かを知ることができます。
では８回目の配達は何日でしょうか？
初日から３を足すやり方は捨てて、「順番」と「その値」の関係から計算してみます。
第１回目の配達が２日で、それに３を何回足せばいいのか考えます。
８回目は３を（８−１）回足せばいいのですね。
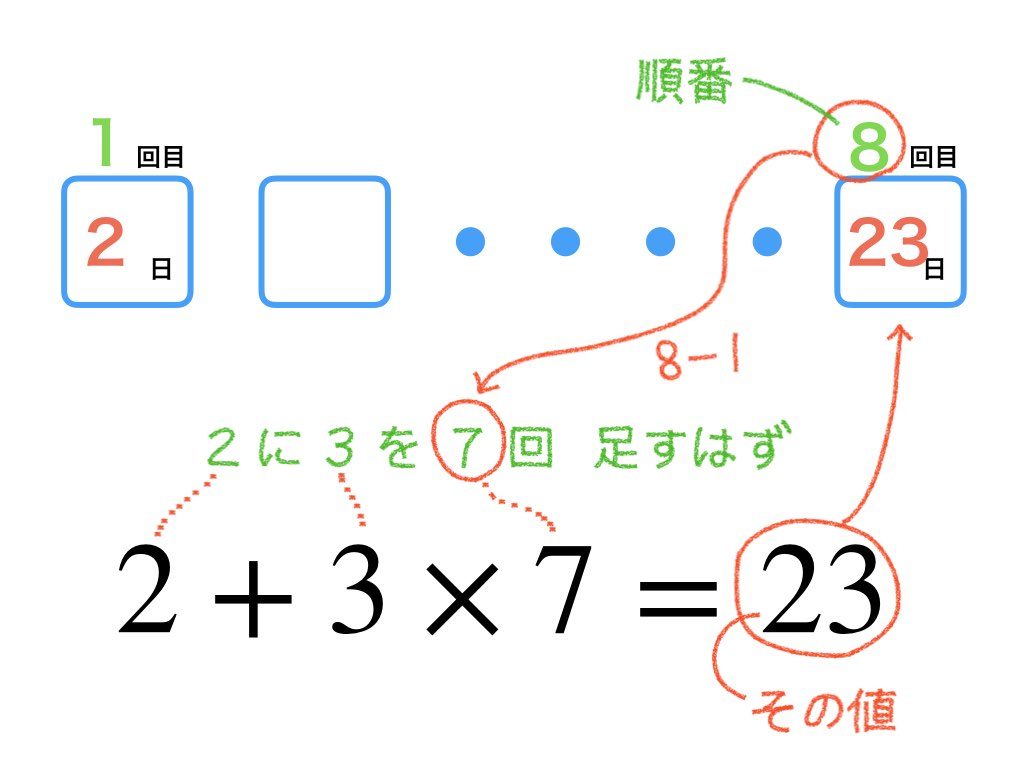
このように順番とその値の関係を知れば式を組み立てることができます。
これは知ってのとおり等差数列の例でしたね。
等差数列の公式をもう一度確認しましょう
さあ、「順番」の話と「その値」の話がわかったところで、もう一度、等差数列一般項を求める公式を確認してみてください。
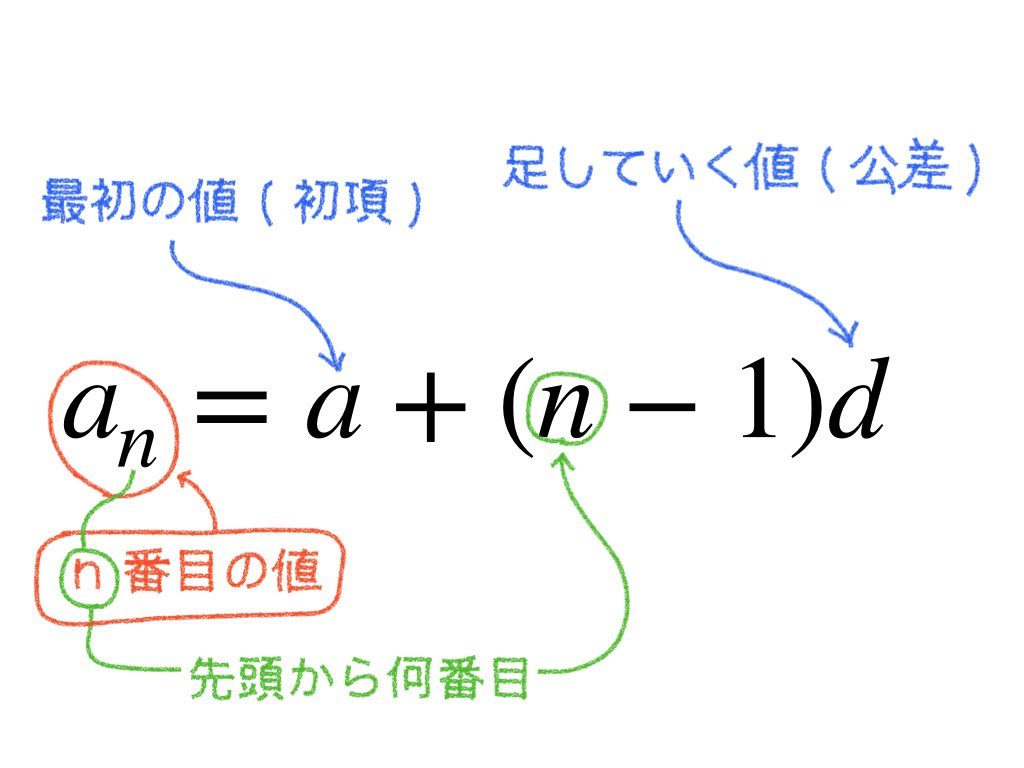
どうでしょうか。今までとは違って見えてきませんか？
「順番」の話と「その値」の話がはっきりと分離できれば、公式の理解がはっきりしてきます。
数列が解けない理由
数列の問題を解くとき、いま「順番」の話をしているのか、それとも「その値」の話をしているのか常に意識してください。
それがはっきりと分離できたら、数列は上手に解くことができます。
【群数列】解き方がわからない！コツはないの？
