【三角関数】公式が多すぎる！全部暗記しなければいけないの？

三角関数には多くの公式が出てきますね。これをすべて暗記するのは大変です。

三角関数を勉強する最初の頃に公式すべてを丸暗記するのは時間の浪費です。それは丸暗記に頼ると、せっかくの三角関数を理解する機会を失ってしまうからです。

三角関数を勉強し始めたときは、ひとつひとつの公式がどのように成り立っているのか、公式を導き出す方法を身につけた方が後の勉強に活きます。

ここでのポイントは単位円上の点の移動です。

【スタディサプリ】動画授業で苦手を克服

三角関数の定義を確認しよう

三角関数の定義を確認しましょう。

原点を中心にして半径１の円を単位円といいます。円の中心は原点に置きます。

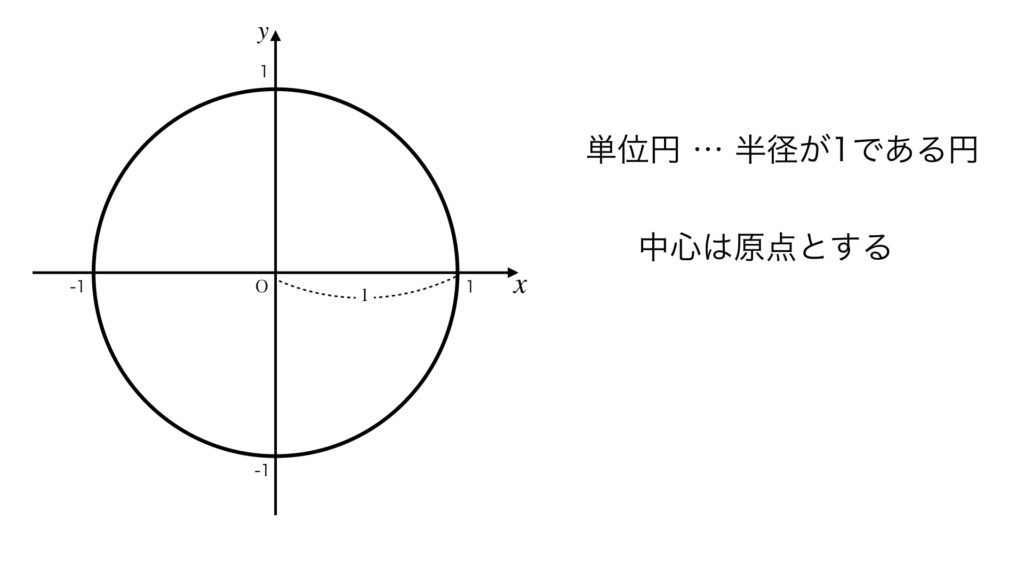
単位円にすれば、三角関数の定義により、円周上の点の座標で三角関数の値がわかります。 x 座標は cos θ の値、y 座標は sin θ の値です。tan θ の値は 定義により y 座標 ÷ x 座標です。

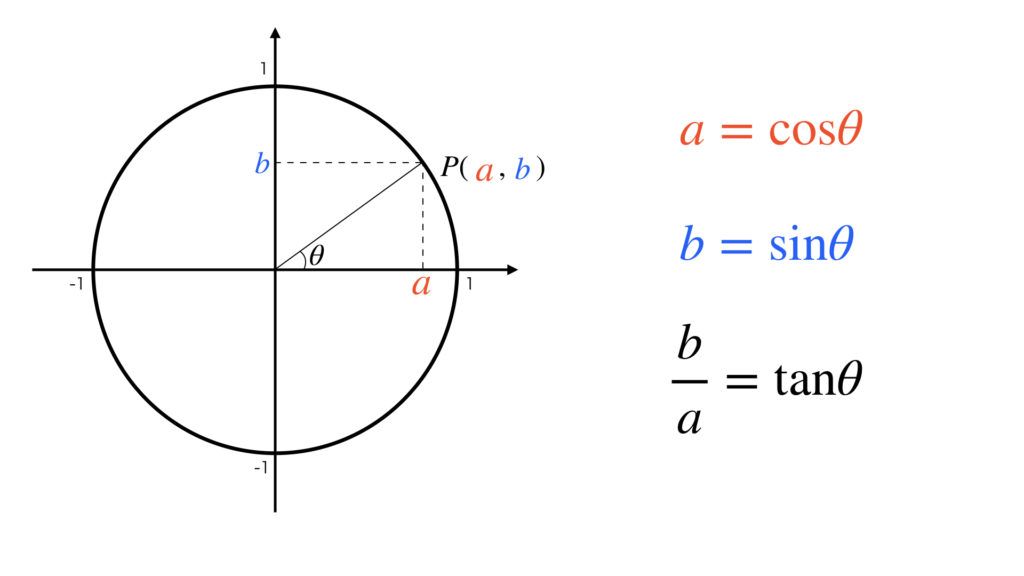
これらが三角関数の出発点です。

ここでは弧度法を用いて角度を表します。

【三角関数】弧度法って何なの？度数法ではダメなの？

ーθ の三角関数

では公式を確認していきましょう。最初は ーθ の関数です。

動径の回転には、時計の針と逆向きの正の向き、時計の針と同じ向きの負の向きがあります。

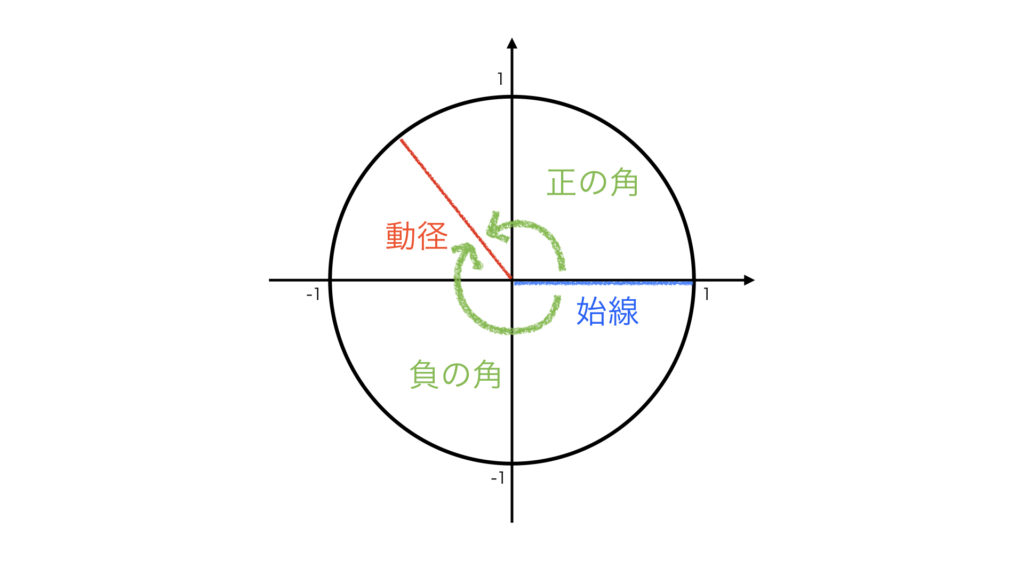
動径を始線から負の向きに θ だけ回転させた回転角が ーθ です。 点 P を原点に対してーθ 回転移動した点 P’ の座標を読み取ります。

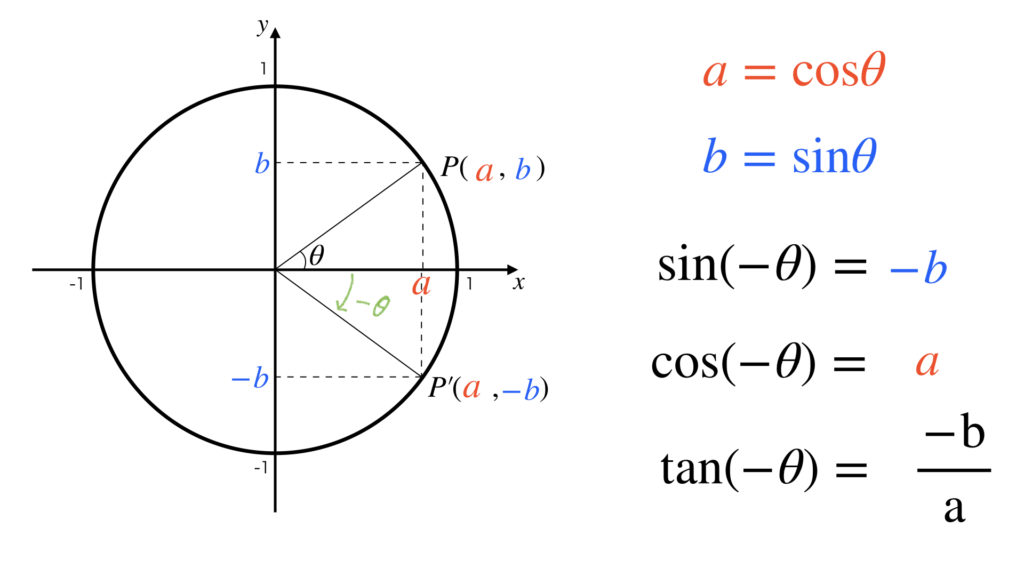
これは x 軸に対する対称移動と同じであることに着目してください。

x 座標を読み取れば cos θ の値、y 座標を読み取れば sin θ の値でしたね。tan θ は y 座標 ÷ x 座標 です。

よって次の公式が導けます。

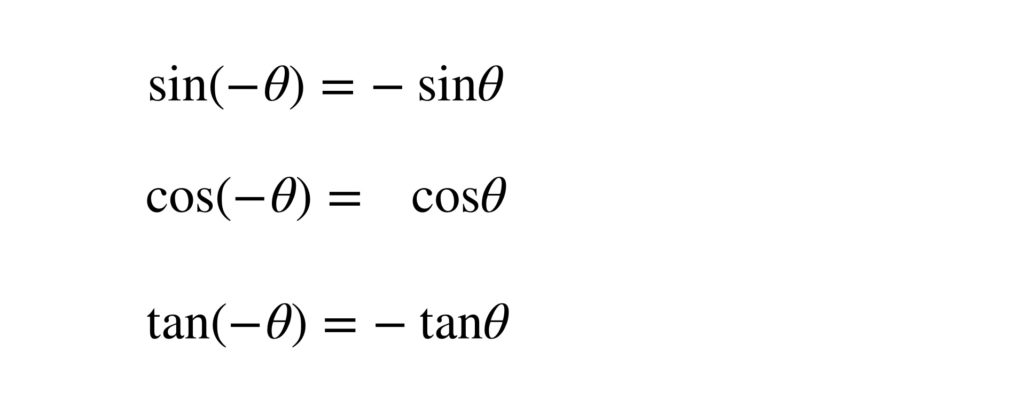
θ ＋ π の三角関数

次は θ + π の三角関数の公式です。

π の回転移動は原点に対しての対称移動と同じです。点 P を原点に対して対称移動した点を P’ として、その x 座標と y 座標を読み取ります。

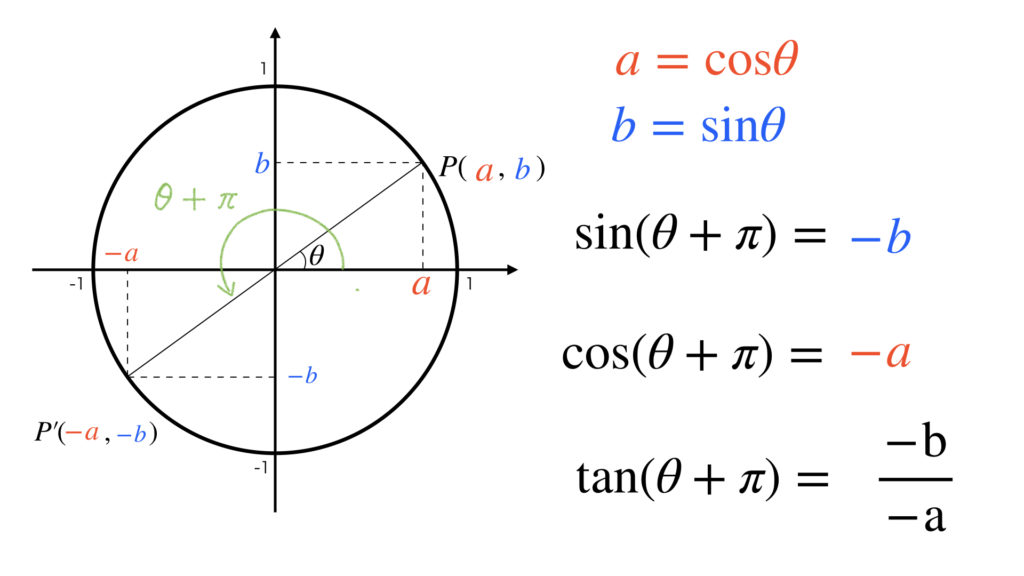
よって次の公式が求まります。

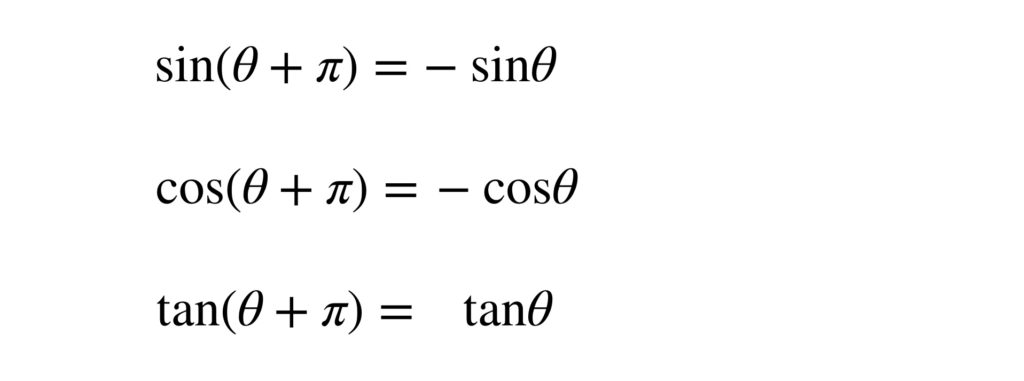
θ ＋ π / 2 の三角関数

下の図で斜線を引いた三角形に着目してください。θ の角度の動線を π / 2 正の向きに回転移動させ合同な三角形を図のように描きます。三角形の辺の長さに注意して点P’の x 座標と y 座標を読み取ります。

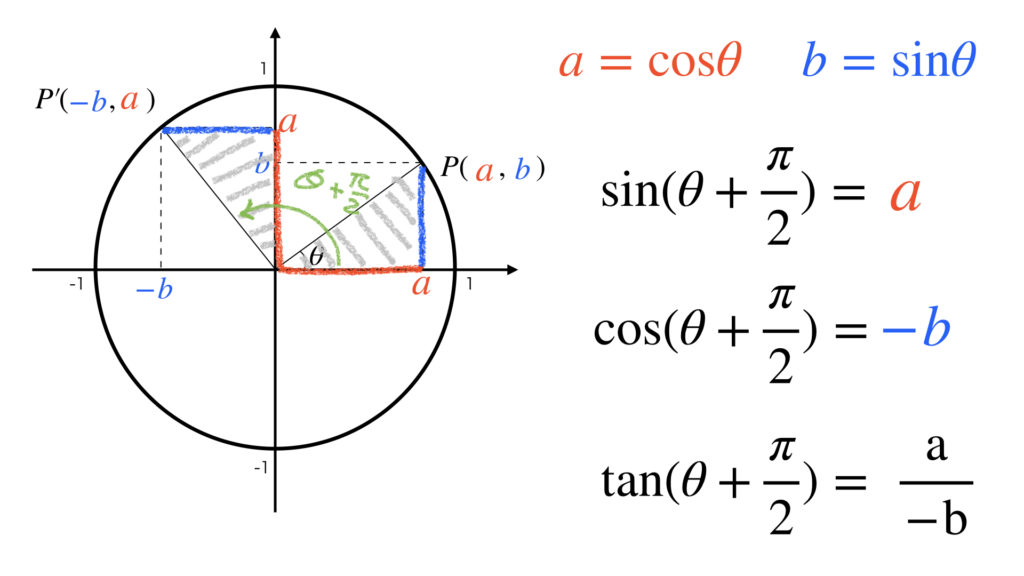
これらにより次の公式が成り立ちます。

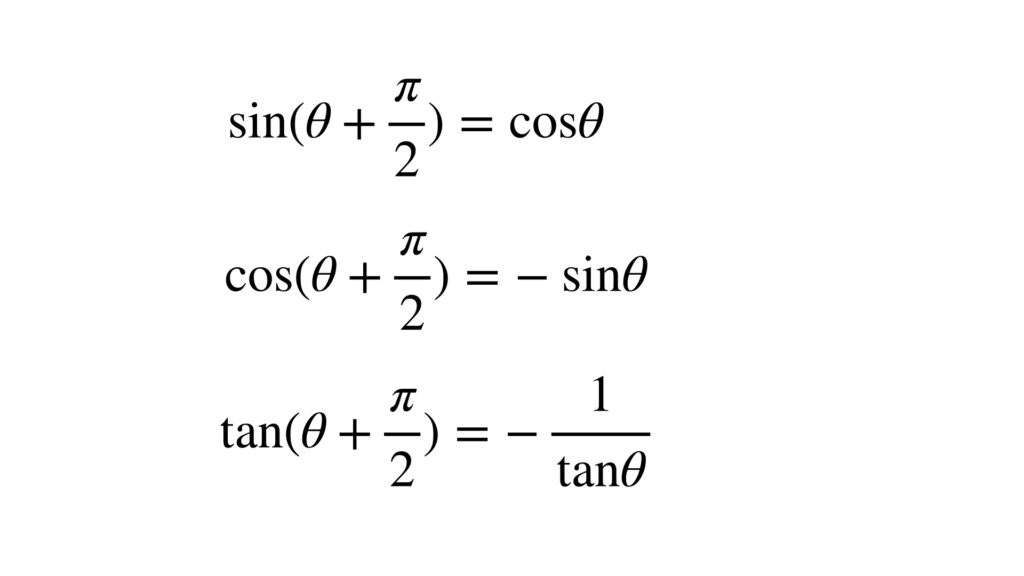
π / 2 − θの三角関数

下の図でグレーで斜線を引いた三角形に着目してください。角度 π / 2 から− θ 回転させれば π / 2 − θ の角度です。三角形の辺の長さに注意して点P’の x 座標と y 座標を読み取ります。これは x 座標の値と y 座標の値が入れ替わっているので、直線 y = x に対する線対称移動と同じです。

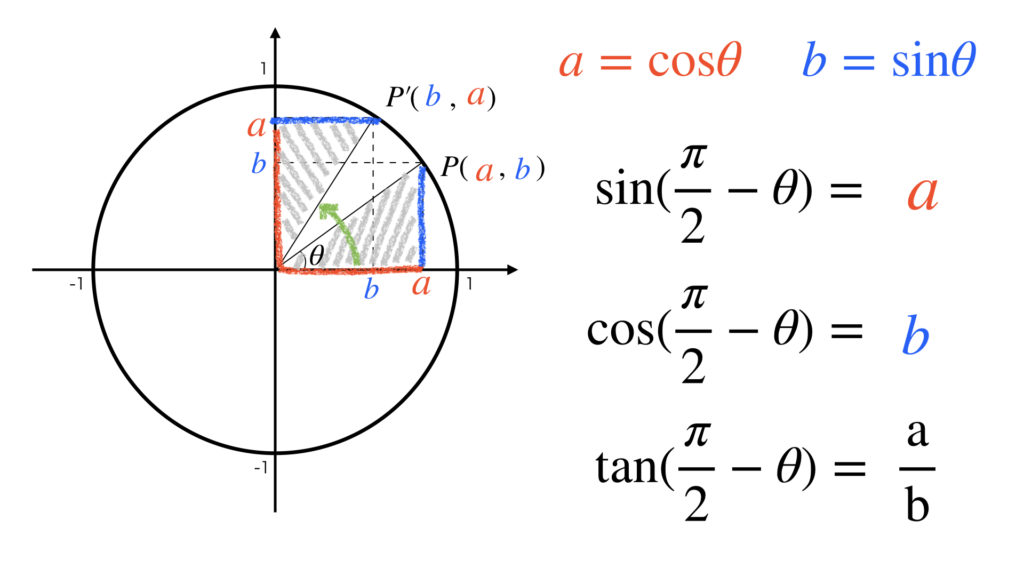
これらにより次の公式が成り立ちます。

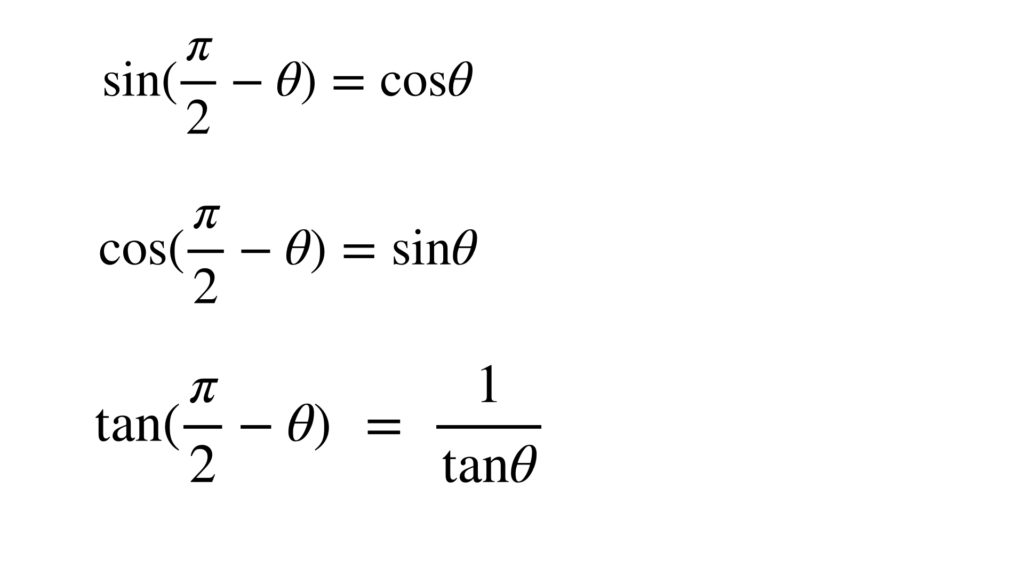
まとめ

三角関数の公式は、単位円上の点を回転移動させ、移動した点の座標を読みとることで導き出されます。使い慣れてくると頭の中で自然とイメージできるようになります。最初のうちは公式の丸暗記に頼らず、単位円上の点の移動で考えられるようになりましょう。